Книги
Больше денег: что такое Ethereum и как блокчейн меняет мир
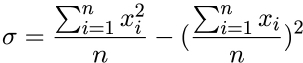
А вот Джини:
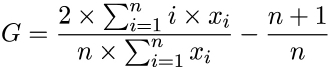
Он куда безобиднее, чем кажется, честно!
Что же не так с коэффициентом Джини? На самом деле много чего. Его недостатки описаны во множестве статей, так что здесь я сосредоточусь на одном. На мой взгляд, этому изъяну уделяли недостаточно внимания при обсуждении Джини в целом, и он непосредственно связан с анализом неравенства в интернет-сообществах вроде блокчейна. Этот недостаток заключается в том, что коэффициент Джини объединяет в единый показатель неравенства две совершенно разные проблемы: проблему страданий из-за нехватки ресурсов и проблему концентрации власти.
Чтобы лучше понять разницу между этими проблемами, рассмотрим два антиутопических сценария.
▓ Антиутопия А: половина населения поровну делит между собой все ресурсы, а у второй половины не остается ничего.
▓ Антиутопия Б: половина ресурсов попадает в руки одного человека, а население делит оставшееся поровну между собой.
Вот кривые Лоренца (выпуклая диаграмма, которую мы видели выше) для обеих антиутопий.
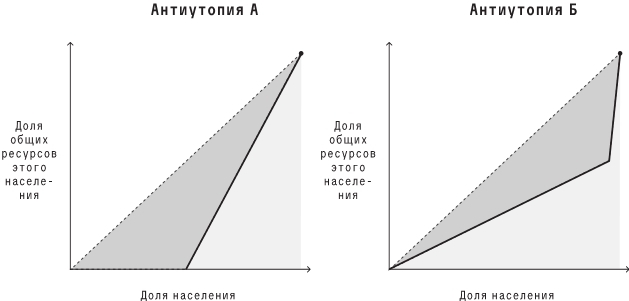
Очевидно, что в обоих мирах жизнь сложится непростая, но непростая по-разному. Житель антиутопии А попадет либо в левую половину с невообразимым и ужасающим массовым голодом, либо в правую, где царит эгалитарная гармония. Если вы Танос[85], вам вполне может там понравиться! В ином случае лучше обходить это место стороной. Антиутопия Б, в свою очередь, напоминает «Дивный новый мир»: у всех вполне достойная жизнь (по крайней мере, на тот момент, когда фиксируются данные о богатстве), но за нее приходится платить крайне недемократической структурой власти, где вся надежда на то, что правитель окажется хорошим. Если вы Кёртис Ярвин[86], вам вполне может там понравиться! В ином случае, опять же, лучше обходить такое место стороной.
Это достаточно разные проблемы, поэтому нужно измерять и анализировать их по отдельности. Причем они различаются не только теоретически. Вот диаграмма, сравнивающая долю общего дохода нижних 20 % (довольно надежный показатель удаленности от антиутопии А) с долей общего дохода верхнего 1 % (довольно надежный показатель приближенности к антиутопии Б).
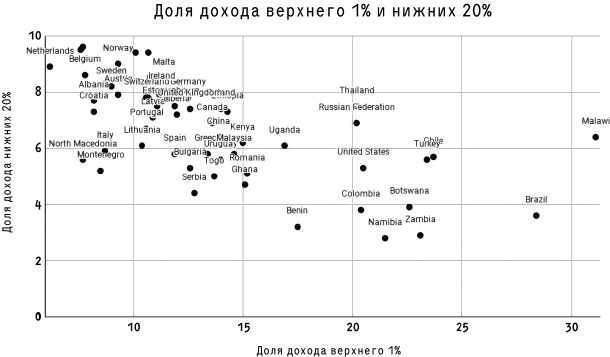
Источники: https://data.worldbank.org/indicator/SI.DST.FRST.20 (смешанные данные за 2015 и 2016 годы) и http://hdr.undp.org/en/indicators/186106
Показатели явно коррелируют (коэффициент –0,62), но очень далеки от идеальной корреляции (верховные жрецы статистики, если я не ошибаюсь, считают 0,7 нижним порогом «высокой корреляции», а мы не добрались даже до него). В диаграмме есть интересное и достойное отдельного анализа второе измерение: в чем разница между страной, где верхний 1 % зарабатывает 20 % от общего дохода, а нижние 20 % – 3 %, и страной, где верхний 1 % зарабатывает 20 %, а нижние 20 % – 7 %? Увы, эти изыскания я лучше оставлю более опытным исследователям данных и культуры.
Проблема концентрации богатства в блокчейне тоже актуальна и заслуживает отдельных измерений и анализа. Это важно для блокчейн-сообщества в целом, поскольку многие люди (и Сенат США на своих слушаниях[87]) пытаются выяснить, действительно ли криптография так антиэлитарна или она просто заменяет старые элиты новыми. Показатель концентрации богатства также важен при сравнении различных криптовалют.
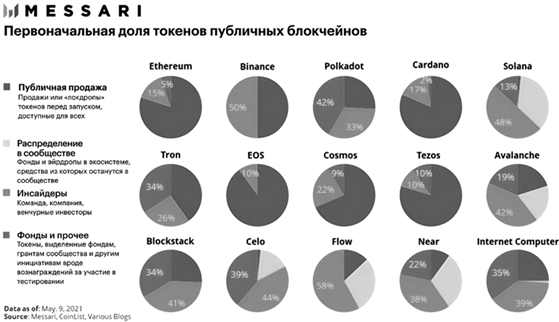
Доля монет первоначального предложения криптовалюты, изначально выделенная отдельным инсайдерам, – один из типов неравенства. Обратите внимание, что данные об Ethereum не совсем точны: доли инсайдеров и фонда должны составлять 12,3 и 4,2 %, а не 15 и 5%
С учетом повышенного внимания к этим проблемам неудивительно, что многие пытались вычислить индексы Джини для криптовалют. И не все результаты оказались так плохи, как уверяла сенсационная статья 2014 года.
Помимо понятных и банальных методологических ошибок (смешивание неравенства в доходах с неравенством в богатстве, смешивание пользователей с учетными записями или и то и другое) использование коэффициента Джини для такого рода сравнений связано с более глубокой и не вполне очевидной проблемой. Эта проблема кроется в ключевом различии между типичными географическими сообществами (например, городами или странами) и типичными интернет-сообществами (например, блокчейном).

Типичный житель географического сообщества тратит бóльшую часть своего времени и ресурсов внутри этого сообщества, поэтому измеряемое неравенство в географическом сообществе отражает неравенство в общем объеме доступных людям ресурсов. Но в интернет-сообществе измеряемое неравенство может происходить из двух источников: первый – неравенство в общем объеме ресурсов, доступных разным участникам, второй – неравенство в уровне заинтересованности в участии в сообществе.
Среднестатистический человек с $15 в фиатной валюте беден и лишен шансов на хорошую жизнь. Среднестатистический человек с $15 в криптовалюте – дилетант, который когда-то открыл кошелек развлеченья ради. Неравенство в уровне интереса не говорит о сообществе ничего плохого; везде есть свои дилетанты и свои фанатики. Поэтому если у криптовалюты очень высокий коэффициент Джини, но при этом бóльшая часть неравенства связана с неравенством в уровне интереса, то за этими показателями вряд ли кроется ужасная реальность, о которой говорят заголовки.
Криптовалюты – даже самые плутократические – не превратят ни одну часть мира во что-то похожее на антиутопию А. Однако плохо распределенные криптовалюты вполне могут походить на антиутопию Б, и проблема усугубится, если решения об изменении протокола будут принимать через голосование монетами. Следовательно, чтобы выявить проблемы, актуальные для криптовалютного сообщества, нам нужно найти метрику, наиболее точно отражающую близость этого сообщества к антиутопии Б.
В качестве альтернативного подхода к измерению неравенства можно сосредоточиться на оценке страданий, вызванных неравномерным распределением ресурсов (то есть проблемой «антиутопии А»). Начнем с некоторой функции полезности, отражающей ценность обладания определенной суммой денег. Популярна log(x), которая совпадает с нашим внутренним ощущением, что практически на любом уровне удвоение дохода одинаково полезно: увеличение с $10 000 до $20 000 добавляет ту же полезность, что и увеличение с $5000 до $10 000 или с $40 000 до $80 000. Таким образом, для оценки неравенства мы измеряем, сколько полезности теряется по сравнению с ситуацией, в которой каждый просто получал бы средний доход:
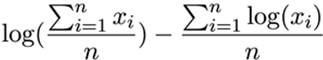
Первое выражение (логарифм среднего значения) – полезность, которую имел бы каждый в случае идеального перераспределения денег, где все получали бы средний доход. Второе выражение (среднее значение логарифма) – средняя полезность, которая сегодня сложилась в этой экономике. Разница между ними – утраченная полезность из-за неравенства, если смотреть на ресурсы именно с точки зрения личного потребления. Существуют и другие подходы к определению этой формулы, но в конечном итоге они практически идентичны (например, в статье Энтони Аткинсона 1969 года была предложена метрика «равномерно распределенного эквивалентного уровня дохода», которая, если U(x) = log(x), представляет собой монотонную функцию вышеупомянутого; а индекс Тейла L идеально математически эквивалентен формуле выше).