▓ Концепция легитимности (принятия высшего порядка) очень сильна. Легитимность появляется везде, где есть координация, и особенно в интернете, где координация присутствует повсюду.

▓ Легитимности можно достичь разными способами, в первую очередь – за счет грубой силы, непрерывности, справедливости, процесса, результата и участия.

▓ Сила криптовалюты в том, что с ее помощью группа людей может накапливать крупные суммы как единое экономическое целое. Это капиталы, которые никогда не принадлежали кому-то конкретному, подчиняются непосредственно концепциям легитимности.

▓ Слишком рискованно начинать финансировать общественные блага, выпуская токены на базовом уровне. Однако, к счастью, Ethereum обладает очень богатой и куда более гибкой экосистемой прикладного уровня. Отчасти это связано с возможностью не только влиять на существующие проекты, но и формировать будущие.

▓ Сообщество должно поддерживать проекты прикладного уровня, которые стремятся развивать общественные блага внутри сообщества, и это очень важно. Пример с DAI[84] показывает, что такая поддержка может сыграть огромную роль!

▓ Экосистема Ethereum неравнодушна к дизайну механизмов и инновациям на уровне общества. Поэтому работа над проблемами финансирования общественных благ внутри самой экосистемы Ethereum стала бы хорошей стартовой точкой!

▓ Но помочь может не только Ethereum. NFT – хороший пример того, как судьба большого капитала зависит от концепций легитимности. Индустрия NFT может стать по-настоящему ценной для художников, благотворительных организаций и других источников общественных благ далеко за пределами нашего виртуального мира. Получится это или нет – зависит от совместных усилий и поддержки сообщества.

Особая благодарность Карлу Флёршу, Айе Миягути и Mr. Silly за идеи, обратную связь и критику.

Против злоупотребления коэффициентом Джини

VITALIK.CA

29 июля 2021 года

Сегодня коэффициент Джини (или индекс Джини), которым обычно измеряют неравенство в доходах или богатстве в отдельной стране, регионе или другом сообществе, – самый известный и популярный показатель неравенства. Это связано с его простотой и возможностью визуализировать его математическое определение в форме графика.

Однако – что ожидаемо для любой схемы, сводящей показатели неравенства к одному числу, – у коэффициента Джини есть свои ограничения. Им стоит пользоваться с осторожностью даже в изначальном контексте – при измерении неравенства доходов и богатства в отдельных странах, – не говоря уже о других областях (в частности, о криптовалюте). В этой статье я расскажу о некоторых ограничениях коэффициента Джини и предложу несколько альтернатив.

ЧТО ТАКОЕ КОЭФФИЦИЕНТ ДЖИНИ?

Коэффициент Джини – это показатель неравенства, предложенный Коррадо Джини в 1912 году. Обычно им измеряют неравенство доходов и богатства в отдельных странах, хотя все чаще пользуются и в других контекстах.

Существуют два равнозначных определения коэффициента Джини.

▓ Определение как области над кривой: нарисуем график функции, где f(p) равняется доле общего дохода, получаемого самой низкооплачиваемой частью населения (например, f(0,1) – доля общего дохода, получаемого 10 % с самым низким доходом). Коэффициент Джини – это область между кривой и линией y = x, которая измеряется как доля от всего треугольника.

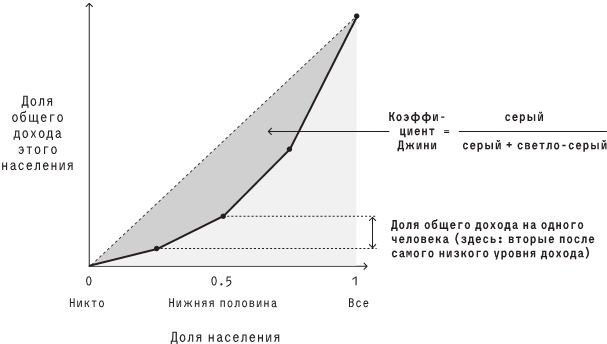
▓ Определение через среднюю разницу: коэффициент Джини равен половине средней разницы в доходах между всеми возможными парами людей, разделенной на средний доход.

Например, на графике выше у нас есть четыре показателя дохода [1, 2, 4, 8], так что есть 16 возможных различий между ними [0, 1, 3, 7, 1, 0, 2, 6, 3, 2, 0, 4, 7, 6, 4, 0]. Следовательно, средняя разница составляет 2,875, а средний доход – 3,75, так что Джини =

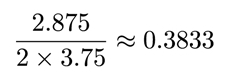
Получается, что эти определения математически эквивалентны (читатель может поупражняться в доказательстве этого утверждения)!

ЧТО НЕ ТАК С КОЭФФИЦИЕНТОМ ДЖИНИ?

Коэффициент Джини любят за то, что это достаточно простой и понятный статистический показатель. Может показаться, что он совсем не простой, но, поверьте, так выглядит практически вся статистика, связанная с произвольной численностью населения (а часто даже хуже). Вот, например, формула совершенно обыкновенного стандартного отклонения: