Рациональность требует, чтобы мы отличали истину от того, что нам хочется ею считать, — чтобы мы не прятали голову в песок, не строили воздушных замков и не называли зеленым виноград, до которого не можем дотянуться. Соблазн магического мышления и стремления выдавать желаемое за действительное всегда с нами, поскольку удача наша полностью зависит от обстоятельств внешнего мира, которых мы просто не в состоянии знать наверняка. Чтобы не падать духом и избегать болезненных мер, которые могут оказаться излишними, мы склонны видеть то, что нам хочется видеть, и закрывать глаза на остальное. Мы балансируем на краешке весов в ванной, чтобы цифры на дисплее были пониже, откладываем медицинское обследование, результат которого может нас расстроить, и стараемся верить, что природа человека бесконечно пластична.

Но есть и более рациональный способ примирить наши желания с нашим неведением — этот инструмент разума называется теорией обнаружения сигнала, или теорией статистических решений. Она объединяет основные идеи двух предыдущих глав: как оценить вероятность, что некоторое утверждение касательно состояния окружающего мира истинно (байесовское мышление), и как решить, что с этим делать, взвешивая ожидаемые издержки и выгоды (рациональный выбор)[285].

Сложность с обнаружением сигнала заключается в том, чтобы понять, должны ли мы считать изменение некоторого показателя настоящим сигналом от внешнего мира — или же шумом, возникшим вследствие несовершенства человеческого восприятия. В жизни мы регулярно сталкиваемся с этой дилеммой. Дежурный офицер видит точку на экране радара. Что это — нас атакует ядерный бомбардировщик или мимо летит стая чаек? Рентгенолог замечает на снимке затемнение. У пациента раковая опухоль или же доброкачественная киста? Присяжные слушают показания очевидца. Подсудимый виновен или же очевидец заблуждается? Мы встречаем человека, который кажется нам смутно знакомым. Мы уже встречали его или это внезапный приступ дежавю? Группе пациентов стало лучше после приема лекарства. Лекарство работает или мы наблюдаем эффект плацебо?

Пользуясь теорией статистических решений, мы получаем не степень уверенности, но решение, что предпринять: согласиться или отказаться от операции, осудить обвиняемого или оправдать его. Принимая ту или иную сторону, мы не выбираем, каким утверждениям о состоянии мира верить. Мы решаем, что нам делать, принимая во внимание предполагаемые издержки и выгоды. Этот когнитивный инструмент заставляет нас осознать разницу между «что истинно» и «что делать». Признавая тот факт, что разные внешние обстоятельства подталкивают нас к разным вариантам рискованного выбора, теория помогает понять, что нам не нужно обманываться, чтобы выбрать что-то одно. Проведя четкую грань между тем, как мы оцениваем состояние внешнего мира, и тем, что мы решаем по этому поводу предпринять, мы можем рационально действовать так, как если бы некое знание было истинным, причем верить в его истинность при этом не обязательно. Как мы убедимся далее, такой подход заставляет совершенно по-новому взглянуть на применение статистики в науке, причем этому факту редко уделяется должное внимание.

Сигналы и шум, да и нет

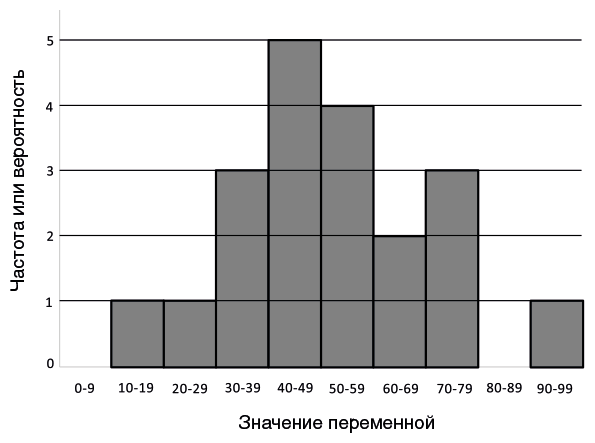
Как нам относиться к какому-нибудь ненадежному индикатору состояния внешнего мира? Начнем с понятия статистического распределения[286]. Допустим, мы измеряем какой-то показатель, который непредсказуемо варьирует («случайную переменную»), вроде баллов от 0 до 100, набранных в тесте на интроверсию. Мы распределяем результаты по диапазонам — от 0 до 9, от 10 до 19 и так далее — и подсчитываем число испытуемых, чьи результаты попали в каждый из них. Теперь представим эти данные в виде гистограммы — графика, который отличается от привычных тем, что интересующая нас переменная откладывается по горизонтали, а не по вертикали. Вертикальный размер тут — это просто число испытуемых, попавших в каждый из диапазонов. Перед нами гистограмма, показывающая, как распределились баллы, набранные двадцатью испытуемыми в тесте на интроверсию, — один человек соответствует одному прямоугольнику.

Теперь представьте, что мы протестировали несколько миллионов человек — достаточно, чтобы не сортировать их результаты по диапазонам, а просто разместить на горизонтальной оси слева направо согласно набранным баллам. По мере того как мы накапливаем все больше данных и отходим все дальше от плоскости графика, зиккурат с предыдущей картинки превращается в плавный изгиб — знакомую колоколообразную кривую, которую вы видите ниже. Максимальное количество результатов скапливается в центре, в районе средних значений переменной, а левее, где значения все ниже, и правее, где они все выше, результатов все меньше и меньше. Самая известная математическая модель колоколообразной кривой называется нормальным распределением, или распределением Гаусса.

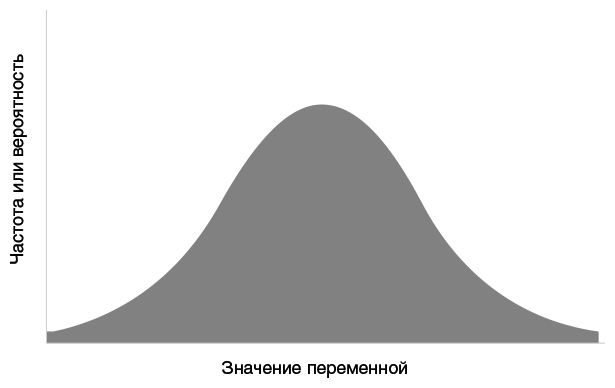
Колоколообразные кривые встречаются в мире на каждом шагу — так распределяются баллы, набранные в личностных тестах или тестах на уровень интеллекта, рост мужчин и женщин, скорость автомобилей на трассе. Такие кривые — не единственный вариант распределения результатов наблюдения. Существуют двухвершинные (они же бимодальные) распределения, например относительный уровень сексуального влечения мужчин к женщинам и к мужчинам, с высоким пиком с одного краю для гетеросексуалов и низким пиком с другого для гомосексуалов, а также небольшим числом бисексуалов посредине. Существуют и распределения с толстым хвостом, где крайние значения редки, однако не астрономически редки, — так выглядят, например, распределения городов по численности населения, граждан по уровню доходов или веб-сайтов по числу посетителей. У многих из таких распределений, например у тех, что возникают вследствие «степенной зависимости», слева имеется высокий хребет с большим числом низких значений переменной, а справа — длинный толстый хвост с толикой экстремально высоких значений[287]. Но колоколообразные распределения — одновершинные, симметричные, с тонкими хвостами — являются самыми обычными; они возникают всегда, когда измеряемая величина представляет собой суммарный эффект огромного числа мелких причин, например множества генов и одновременно множества факторов внешней среды[288].

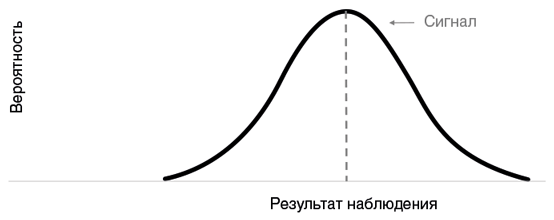
Теперь обратимся к нашей теме — к наблюдениям, случилось ли что-либо в реальности или нет. Абсолютное знание нам недоступно: мы не бог и можем полагаться лишь на результаты измерений — на точки на экране радара, засекшего самолет, или затемнения на снимке, вызванные опухолью. Результаты эти раз от раза не совсем одинаковы. Они, как правило, распределяются по колоколообразной кривой, как показано на рисунке ниже. Этот график можно считать графиком байесовского правдоподобия, то есть вероятности такого результата наблюдений при условии наличия сигнала[289]. В среднем у результата наблюдений есть определенное значение (вертикальная пунктирная линия), но иногда он чуть выше или чуть ниже.

Но вот трагическая загвоздка: можно было бы подумать, что если в окружающем мире ничего не произошло — никакого бомбардировщика и никакой опухоли, то и результаты измерений будут нулевыми. К сожалению, так никогда не бывает. В измерения всегда вкрадываются шумы — электростатический заряд, птичья стая, доброкачественная киста, видная на снимке, причем и они тоже меняются от измерения к измерению, формируя собственную колоколообразную кривую. Что еще печальнее, верхний диапазон измерений, регистрирующих шум, может накладываться на нижний диапазон измерений, регистрирующих реальные явления:

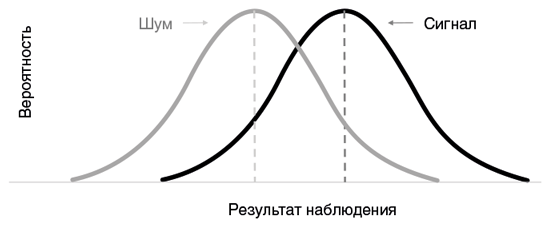
Трагедия в том, что видеть эту диаграмму и знать, чем вызван наблюдаемый феномен — сигналом или шумом, может только Господь бог. Все, что видим мы, смертные, — это результаты наших наблюдений:

Когда мы вынуждены догадываться, что представляет собой наблюдаемый феномен — сигнал (реальное явление) или шум (помеха в наших наблюдениях), нам не обойтись без какого-то порога отсечения. На языке теории обнаружения сигнала он называется критерием принятия решения и обозначается символом β (бета). Если результат наблюдения превышает этот критерий, мы говорим «да» и действуем, как если бы зарегистрировали сигнал (так это на самом деле или нет, узнать мы не можем); если результат недотягивает до него, мы говорим «нет» и действуем, как если бы это был посторонний шум:

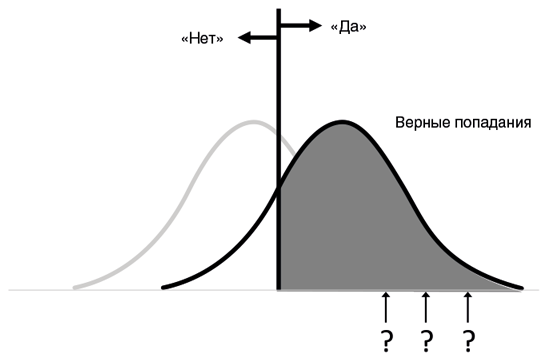
Теперь давайте вернемся к восприятию бога и посмотрим, как хорошо мы в среднем справляемся с задачей обнаружения сигнала, применяя такой порог отсечения. Тут есть четыре варианта. Когда мы говорим «да» и это действительно сигнал (бомбардировщик или опухоль есть), это называется верным попаданием; доля сигналов, которые мы в этом случае правильно обнаруживаем, показана как затемненная область распределения.

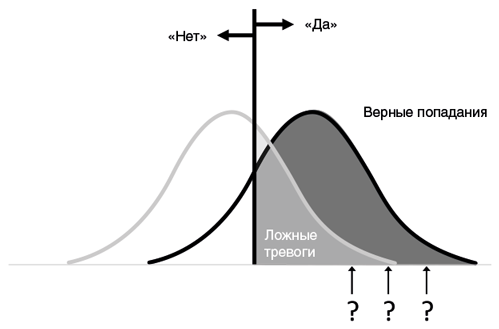
Но что, если это просто шум? Если мы говорим «да», а сигнала на самом деле не было, это называют ложной тревогой; доля моментов, когда мы зря схватились за пистолет, выделена светло-серым.

Но что случается, если результат наблюдения недотягивает до критерия и мы говорим «нет»? И снова здесь может быть два варианта. Когда что-то действительно случилось, а мы этого не заметили, это называют промахом. Когда же мы безошибочно определили посторонний шум, это называют правильным отрицанием.

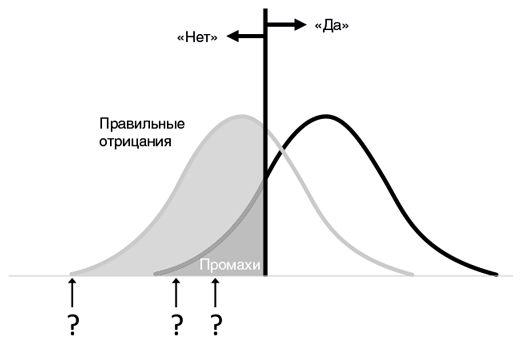
Вот как эти четыре варианта делят между собой пространство событий:

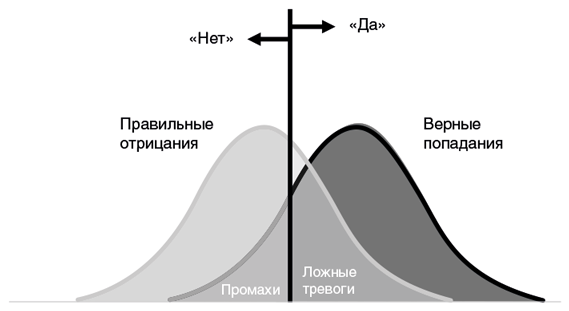
Так как мы всякий раз говорим либо «да», либо «нет», доли верных попаданий и промахов при наличии сигнала (правая кривая) должны в сумме составлять 100 %. Аналогичной должна быть и сумма долей ложных тревог и правильных отрицаний при регистрации шума (левая кривая). Если сдвигать критерий принятия решения влево (понижать) и стрелять с меньшей осмотрительностью или сдвигать его вправо (повышать) и пореже хвататься за оружие, мы меняем соотношение верных попаданий и промахов события, а также ложных тревог и правильных отрицаний — это чистая арифметика. Что менее очевидно, поскольку эти две кривые накладываются одна на другую, мы к тому же меняем соотношение между верными попаданиями и ложными тревогами (в тех случаях, когда мы говорим «да»), а также промахами и верными отрицаниями (когда говорим «нет»). Давайте посмотрим, что произойдет, если мы ослабим критерий принятия решения, то есть станем чаще хвататься за оружие и говорить «да»:

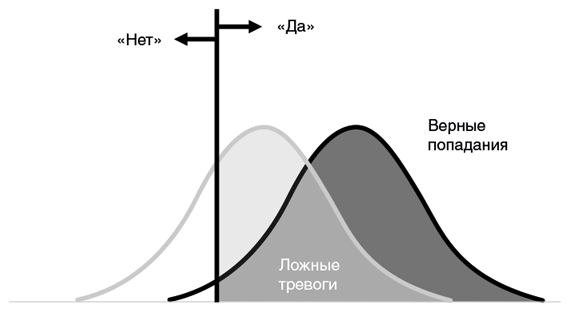
Хорошие новости: верных попаданий стало больше — мы ловим практически каждый сигнал. Плохие новости: ложных тревог тоже стало больше — мы хватаемся за пистолет чуть ли не при каждой фиксации постороннего шума. А что будет, если мы, наоборот, введем более жесткий критерий, станем осторожнее, будем чаще говорить «нет» и требовать доказательств понадежнее?