Пятая аксиома, аксиома независимости, также довольно занимательна. Если вы отдаете предпочтение А перед В, тогда вы должны предпочитать лотерею, в которой можно выиграть А или С, лотерее, в которой можно выиграть В или С (если вероятность выигрыша одинакова). То есть шанс получить С в обоих вариантах не должен менять ваших предпочтений. Можно сказать иначе: то, как вы преподносите выбор, как задаете его в контексте, не должно играть никакой роли. Роза, как ее ни назови, будет пахнуть так же сладко. Рациональному субъекту положено фокусироваться на самом выборе и не позволять отвлекающим факторам, присущим обоим вариантам, сбивать его с толку.

Независимость от нерелевантных альтернатив (так в общем виде называется аксиома независимости) — требование, обозначенное в большинстве теорий рационального выбора[250]. Проще говоря, если, выбирая между А и В, вы отдаете предпочтение А, вы не можете выбрать В просто потому, что к выбору добавили какую-нибудь третью опцию, С. Рассказывают, как логик Сидни Моргенбессер (с которым мы уже встречались в главе 3) сидел однажды в ресторане, и ему предложили выбор между яблочным и черничным пирогом. Он выбрал яблочный, но вскоре официантка вернулась и сообщила, что сегодня в меню есть еще и вишневый пирог. Словно всю жизнь ждал этого момента, Моргенбессер ответил: «Ну, тогда я возьму черничный»[251]. Если анекдот вас рассмешил, значит, вы понимаете, почему независимость от нерелевантных альтернатив служит критерием рациональности.

Шестая аксиома — аксиома последовательности: если вы предпочитаете А, а не В, то гарантированному получению В вы предпочтете лотерею, по условиям которой с определенной вероятностью вы получаете А, а в противном случае — В. Полшанса лучше, чем ничего.

Последнюю аксиому можно назвать аксиомой взаимозаменяемости: она описывает поиск баланса между силой желания и вероятностью его осуществить[252]. Если субъект предпочитает А, а не В, и В, а не С, существует такое значение вероятности, при котором ему будет безразлично, что выбрать: гарантированное В (второе по предпочтительности) или лотерею, где с указанной вероятностью выигрыш принесет А (приоритетный выбор), а проигрыш — С. Чтобы это прочувствовать, представьте, что вероятность выиграть А высока — 99 %, а шанс удовольствоваться С — всего 1 %. При таком раскладе разумнее рискнуть, чем смириться со второй по предпочтительности опцией, В. Теперь представьте себе другую крайность: по условиям лотереи вероятность выиграть А равна 1 %, а шанс остаться с С, которое вам нравится меньше всего, составляет 99 %. Теперь все наоборот: гарантированный компромисс, В, уверенно бьет вариант, в котором вы почти наверняка получите самое неинтересное вознаграждение. Теперь представьте ряд вероятностей от «почти наверняка А» до «почти наверняка С». Если вам кажется, что, по мере того как шансы плавно меняются, сначала лотерея кажется заманчивей, потом вам все равно, рискнуть или сразу взять В, а ближе к концу вы безропотно соглашаетесь на В, значит, вы согласны с рациональностью аксиомы взаимозаменяемости.

Что же следует из этой теории? Чтобы удовлетворять перечисленным критериям рациональности, субъект, принимающий решение, должен прикинуть ценность каждого исхода на непрерывной шкале желательности, умножить ее на вероятность этого исхода и суммировать все полученные произведения, вычислив «ожидаемую полезность» всего выбора. (В этом контексте «ожидаемая» означает «средняя в долгой перспективе», а не «предвкушаемая», а «полезность» означает «предпочтительность по мнению выбирающего», а не «пользу» или «практичность».) Вычисления не обязательно должны быть сознательными или выраженными в цифрах — они могут представлять собой качественные представления. В итоге субъект, принимающий решение, должен выбрать вариант с наивысшей ожидаемой полезностью. Это гарантирует, что выбор будет рациональным согласно всем семи критериям. Тот, кто выбирает рационально, максимизирует полезность; также верно и обратное.

Рассмотрим это на конкретном примере. Допустим, вы находитесь в казино и думаете, во что бы вам сыграть. В игре в кости вероятность выпадения семерки составляет 1 к 6, а выигрыш принесет вам 4 доллара; в случае проигрыша вы лишитесь 1 доллара, уплаченного за участие в игре. Будем считать, что полезность исчисляется в долларах. Тогда ожидаемая полезность ставки на семерку при игре в кости составит (1/6 × 4$) + (5/6 × (–1$)), или –0,17 долларов. Сравним с рулеткой. Вероятность выпадения семерки — 1 к 38, и, если она выпадет, вы выиграете 35 долларов; в противном случае зря потратите тот же самый 1 доллар. Ожидаемая полезность игры в рулетку составляет (1/38 × 35$) + (37/38 × (–1$)), то есть –0,05 долларов. Ожидаемая полезность ставки на семь при игре в кости ниже, чем при игре в рулетку, так что никто не назовет вас нерациональным, если вы выберете рулетку. (Безусловно, найдутся такие, кто назовет вас нерациональным потому, что вы вообще играете в азартные игры, поскольку ожидаемая полезность обеих ставок отрицательна: игорный дом взимает свою плату, так что чем дольше вы играете, тем больше проигрываете. Но раз уж вы явились в казино, значит, атмосфера Монте-Карло и трепет неизвестности обладают для вас некоторой положительной полезностью, которая сдвигает суммарную полезность обоих вариантов в область положительных чисел, и вам остается только выбрать игру.)

Азартные игры — пример, на котором проще всего объяснять теорию рационального выбора: они обеспечивают нас точными числами, которые можно умножать и складывать. Но обыденная жизнь подсовывает нам бесчисленные ситуации выбора, который мы также интуитивно оцениваем в терминах ожидаемой полезности. Я стою в супермаркете и безуспешно пытаюсь вспомнить, есть ли дома молоко; может, мне стоит купить пакет? Я подозреваю, что молоко закончилось; если это действительно так, а я откажусь от покупки, утром мне придется завтракать кукурузными хлопьями всухомятку. С другой стороны, если молоко в холодильнике осталось, а я куплю еще, худшее, что может случиться, — молоко прокиснет, что маловероятно; но даже если и так, я впустую потрачу всего лишь пару долларов. Так что лучше я все-таки куплю молока. Теория рационального выбора просто-напросто раскрывает смысл такого рода размышлений.

Насколько полезна полезность?

Соблазнительно думать, что модели предпочтений, описываемые аксиомами рациональности, отражают субъективные человеческие ощущения удовольствия и желания. Но, строго говоря, аксиомы рационального выбора считают принимающего решения субъекта черным ящиком и учитывают только правила, согласно которым он предпочитает одну альтернативу другой. Шкала полезности, которая тут фигурирует, — воображаемая, она выведена из данной модели предпочтений и предлагается в качестве способа сделать эти предпочтения последовательными. Теория рационального выбора защищает субъекта, который принимает решения, от развода на деньги, неспособности выбрать десерт и прочих нелепых положений. Соответственно, она не столько диктует нам, как действовать в согласии с нашими ценностями, сколько объясняет, как эти самые ценности прояснить, наблюдая за собственным поведением.

Это соображение отправляет в утиль первое из ложных представлений о теории рационального выбора: будто она изображает людей аморальными гедонистами или, что еще хуже, советует им такими стать. Полезность не равна личной выгоде; это любая ценность, которую последовательно максимизирует рационально выбирающий субъект. Если люди приносят жертвы ради своих детей и друзей, если они ухаживают за больными и подают милостыню бедным, если они возвращают бумажники, набитые деньгами, это лишь доказывает, что любовь, милосердие и честность вписаны в их шкалу полезности. Теория же рационального выбора подсказывает, как не спустить эти свои ценности в трубу.

Конечно, обдумывая принятие решений, мы не обязаны считать себя черными ящиками. Гипотетическая шкала полезности должна соответствовать нашим внутренним ощущениям радости, алчности, вожделения, нежности и прочих страстей. Однако, исследуя эту взаимосвязь на конкретных примерах, начиная с самого очевидного объекта желаний — денег, мы натыкаемся на интересный факт. Независимо от того, можно ли купить счастье за деньги или нельзя, за деньги точно можно купить полезность, поскольку все полезные вещи (даже благотворительность) люди оплачивают деньгами. При этом зависимость полезности от денег не линейна — график ее выпуклый. Выражаясь профессиональным языком, мы имеем здесь дело с «убывающей предельной полезностью».

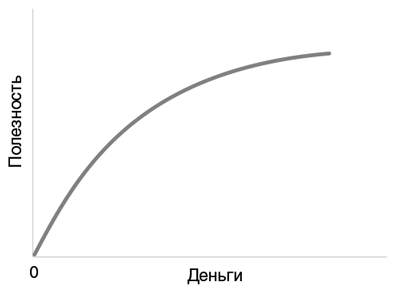
Психологический смысл этого очевиден: лишние сто долларов принесут бедняку больше радости, чем богачу[253]. (Это, кстати, хороший этический аргумент в пользу перераспределения богатств: при прочих равных перетекание денежных средств от богатых к бедным увеличивает суммарный уровень счастья.) В теории рационального выбора эта кривая возникает из неочевидного источника: ученые не спрашивают людей с разным уровнем доходов, насколько те счастливы, но изучают их предпочтения. Что бы вы выбрали: 1000 долларов наверняка или лотерею с 50 %-ной вероятностью выиграть 2000 долларов? Ожидаемая выгода обеих альтернатив одинакова, но большинство выбирает гарантированную сумму. Это не значит, что людское поведение противоречит теории рационального выбора; это значит, что полезность не эквивалентна выгоде в долларах. Полезность 2000 долларов в этом примере меньше удвоенной полезности 1000 долларов. К счастью для нашего понимания, восприятие людьми своего удовлетворения и выбор ими лотерей указывают на одну и ту же выпуклую кривую, связывающую деньги и полезность.

Экономисты считают, что выпуклая кривая полезности соответствует «склонности к избеганию риска». Это несколько сбивает с толку, потому что «избегать риска» в данном контексте не значит быть робкой овечкой в противоположность отчаянному сорвиголове, а лишь отражает тот факт, что люди предпочитают гарантированное вознаграждение лотерее с той же ожидаемой выгодой. И все же два эти представления нередко совпадают. Мы покупаем страховку, чтобы обеспечить себе душевный покой, но и бесчувственный рациональный агент, опираясь на кривую полезности, сделал бы то же самое. Покупка страховки сдвигает плательщицу чуть левее по оси денег, что несколько понижает ее уровень счастья, но, если ей придется покупать себе новую машину взамен незастрахованной, сумма на ее банковском счету резко уменьшится, и уровень счастья просядет значительно. Неудивительно, что рациональный агент предпочитает гарантированную потерю некоторой суммы лотерее, в которой можно лишиться гораздо большего, пусть даже ожидаемая выгода гарантированной потери (не путайте с ожидаемой полезностью) должна быть немного ниже, чтобы страховая компания не работала себе в убыток.

К несчастью для теории, по той же логике люди вообще не должны играть в азартные игры, покупать лотерейные билеты, начинать бизнес или стремиться к известности; все должны учиться на дантиста. Однако некоторые люди, конечно же, это делают — парадокс, который не дает покоя экономистам-классикам. Человеческая кривая полезности не может быть одновременно выпуклой, объясняющей, почему мы избегаем риска и покупаем страховые полисы, и вогнутой, объясняющей, почему мы стремимся к риску и играем в азартные игры. Можно, конечно, сказать, что в азартные игры мы играем ради азарта, а страховку покупаем ради душевного спокойствия, но подобная апелляция к эмоциям просто поднимает парадокс на следующий уровень: как так вышло, что эволюция наделила человека конфликтующими мотивами — и заводить себя, и успокаивать, платя деньги за обе привилегии? Может, мы просто нерациональны — и все тут. Может, полуголые танцовщицы, вишенки в бокале и прочий антураж казино — это само по себе развлечение, за которое готовы платить крупные игроки. А может, график имеет точку перегиба и правее уходит резко вверх, вследствие чего ожидаемая полезность джекпота оказывается выше ожидаемой полезности простой прибавки к банковскому счету. Это возможно, если игрок ощущает, что выигрыш способен переместить его в другой социальный класс и обеспечить ему новый образ жизни: гламурного и беззаботного миллионера, а не простого успешного буржуа. Реклама лотерей вовсю играет на подобных фантазиях.

Проанализировать следствия из теории проще всего, когда ожидаемая полезность исчисляется в деньгах, но та же логика применима к любой ценности, которую можно отметить на шкале, в том числе и к ценности человеческой жизни. В высказывании, которое ошибочно приписывают Иосифу Сталину: «Одна смерть — трагедия, миллион смертей — статистика», — указаны неверные числа, и тем не менее оно совершенно точно описывает, как люди обходятся с моральной стоимостью жизней, унесенных бедствиями вроде войн или пандемий. Эта кривая тоже изгибается подобно графику ожидаемой полезности денег[254]. В обычных обстоятельствах СМИ, освещая теракт с дюжиной жертв, звонят во все колокола. Но в разгар войны или пандемии даже тысяча смертей ежедневно воспринимается как должное, несмотря на то что каждая из этих жизней, в отличие от падающего в цене доллара, принадлежала разумному существу, реальному человеку, который любил и которого любили. В книге «Лучшее в нас» (The Better Angels of Our Nature, 2011)^{24} я предположил, что наше морально неоправданное восприятие убывающей предельной полезности людских жизней позволяет мелким войнам разрастаться в гуманитарные катастрофы[255].