Книги
Рациональность. Что это, почему нам ее не хватает и чем она важна
Что это за магия и как она работает? Гигеренцер замечает, что концепция условной вероятности уводит нас прочь от осязаемых, поддающихся подсчету вещей. Все эти доли — 90 % истинно положительных, 9 % ложноположительных, 91 % истинно отрицательных, 10 % ложноотрицательных — не дают в сумме 100 %, и поэтому, чтобы составить пропорцию и вычислить долю истинно положительных результатов от числа всех положительных (эту-то задачу нам и нужно решить), приходится трижды перемножать разные числа. И напротив, если думать о естественной частоте, нетрудно выделить и суммировать все положительные результаты: 9 истинно положительных плюс 89 ложноположительных — это в сумме 98 положительных тестов, а 9 истинно положительных составляют 9 % от этой суммы. (Что человеку
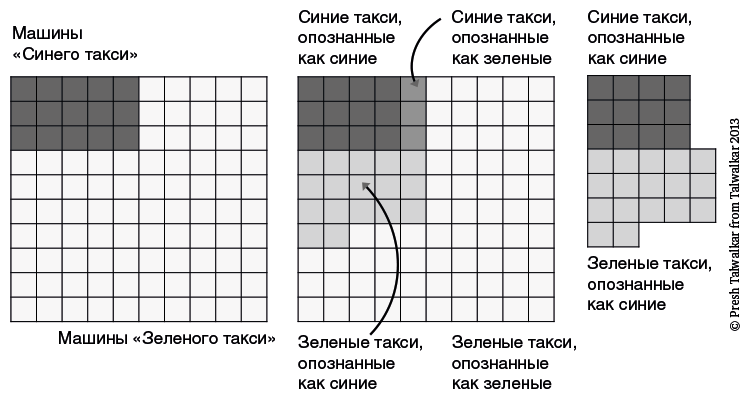
Чтобы еще больше упростить задачу, мы можем задействовать визуальные наклонности нашего обезьяньего мозга и превратить цифры в фигуры. Этот прием делает байесовское рассуждение очевидным; с его помощью можно щелкать даже такие головоломки, как хрестоматийная задачка про такси, хотя она и максимально далека от нашего житейского опыта. Представьте себе весь парк городских такси в виде 100 квадратиков: один квадратик — один автомобиль (на рисунке слева). Закрасим 15 квадратиков в левом верхнем углу — это 15 %, базовая оценка принадлежности к «Синему такси». Чтобы показать четыре варианта показаний нашего свидетеля, которому можно верить на 80 % (на рисунке в центре), мы сделаем чуть светлее три квадратика из тех пятнадцати, что изображают синие такси (20 % от 15 синих такси, которые он сослепу мог спутать с зелеными) и затемним семнадцать квадратиков, изображающих зеленые такси (20 % от 85 зеленых такси, которые он мог ошибочно принять за синие). Свидетель утверждает, что видел синее такси, поэтому мы можем отбросить все такси, которые были опознаны — как верно, так и ошибочно — как зеленые, и у нас остается только самый правый рисунок: одни синие такси (как верно, так и ошибочно опознанные). Теперь с первого взгляда видно, что машины «Синего такси», опознанные как синие, занимают чуть меньше половины площади фигуры. Подсчитаем их для точности: 12 квадратиков из 29, то есть 41 %. Естественная частота и наглядное представление позволяют нам разобраться в имеющихся данных (положительных результатах анализа или такси, опознанных как синие) и разделить их на истинные и ложные.
Если использовать заложенные в нашем мышлении интуитивные представления и переводить данные в удобный для понимания формат, статистические способности широкой публики можно развивать — и не только можно, но и нужно. Умение оценивать риски — навык, необходимый врачам, судьям, государственным деятелям и всем остальным, кому мы вверяем свою жизнь. А учитывая, что мы с вами живем в мире, где бог играет в кости, развитое байесовское мышление и другие виды статистической грамотности — это общественное благо, которое должно стать приоритетом системы образования. Принципы когнитивной психологии подталкивают к выводу, что лучше развивать и обогащать ту рациональность, которая у людей имеется, чем списывать как хронически недееспособных из-за заблуждений и когнитивных искажений чуть ли не всех представителей своего вида[242]. На том же самом настаивают и принципы демократии.
Глава 6. Риск и вознаграждение (рациональный выбор и ожидаемая полезность)
Все жалуются на свою память, но никто не жалуется на свою рассудительность.
Есть теории, которые не вызывают теплых чувств. Вряд ли кто-то питает симпатию к законам термодинамики — недаром поколения вдохновенных чудаков слали в патентные бюро чертежи вечных двигателей. С тех пор как Дарвин сформулировал теорию естественного отбора, креационисты не могут смириться с мыслью, что человек произошел от обезьяны, а коммунитаристы ищут изъяны в постулате о конкуренции как движущей силе эволюции.
Различные версии одной из самых ненавистных теорий современности известны под именами «рациональный выбор», «рациональный агент», «ожидаемая полезность» и
Что же это за недобрая теория? Она гласит, что, оказавшись перед рискованным решением, рациональные агенты должны выбирать вариант, который максимизирует «ожидаемую полезность», то есть сумму потенциальных вознаграждений, взвешенных по их вероятностям. За пределами экономики и некоторых областей политологии эту теорию любят, примерно как Эбенизера Скруджа. Люди понимают ее как заявление, будто человеческие существа являются — или должны быть — эгоистичными психопатами, ну или сверхрациональными бухгалтерами, которые, прежде чем влюбиться, подсчитывают вероятности и полезности. Едва из какой-нибудь психологической лаборатории просочится известие, что поведение людей не удовлетворяет этому описанию, такую новость используют, чтобы поставить под сомнение принципы классической экономической теории, а вместе с ними и целесообразность рыночных подходов[245].
Однако в исходном виде теория рационального выбора представляет собой математическую теорему, которую ценители считают довольно красивой, и в ней ничего не говорится о том, как должны рассуждать и принимать решения представители нашего вида. Многие полагают, что эта теорема дает нам самое строгое определение рациональности — критерий оценки человеческой рассудительности. Как мы увидим далее, это можно поставить под сомнение: порой, когда поведение людей противоречит теории рационального выбора, неясно, люди ли тут нерациональны или предполагаемые стандарты рациональности. В любом случае эта теория проливает свет на загадку рациональности, и, несмотря на свое чисто математическое происхождение, она способна преподать нам несколько важных жизненных уроков[246].
Теория рационального выбора уходит корнями во времена становления теории вероятности, когда Блез Паскаль (1623–1662) сформулировал свой известный аргумент, объясняющий, почему вам стоит уверовать в бога: если вы верите, а бога нет, вы всего-навсего произнесете впустую сколько-то молитв, но, если вы в него не верите, а он есть, вы навлечете на себя его вечный гнев. В 1944 г. математик Джон фон Нейман и экономист Оскар Моргенштерн изложили эту мысль формальным языком. В отличие от папы римского, фон Нейман действительно мог быть инопланетянином — по крайней мере, его коллеги задумывались о такой возможности: фон Нейман был нечеловечески умен. Кроме того, он разработал теорию игр (речь о которой пойдет в главе 8), цифровой компьютер, самореплицирующиеся механизмы, квантовую логику и ключевые компоненты ядерного оружия, а также совершил еще несколько десятков эпохальных открытий в математике, физике и компьютерных науках.
Рациональный выбор — это не психологическая теория, описывающая, как человеческие существа выбирают, и не нормативная теория, указывающая, как они должны выбирать; это теория, объясняющая, как результаты выбора
Красота этой теории в том, что она исходит из горстки простых для понимания аксиом — самых общих требований, которые соблюдает любой принимающий решения субъект, претендующий на звание рационального. После этого она определяет, как этому субъекту нужно принимать решения, чтобы не нарушить эти требования. Аксиомы теории рационального выбора то сливали друг с другом, то по-всякому разделяли; версию, которой я здесь придерживаюсь, сформулировал математик Леонард Сэвидж, а систематизировали психологи Рейд Хасти и Робин Дауэс[247].
Теория рационального выбора
Первую аксиому можно назвать аксиомой соизмеримости: какими бы ни были выборы А и В, человек, принимающий решение, предпочитает либо А, либо В, либо они для него равноценны[248]. Звучит не особенно впечатляюще — это же вроде не более чем здравый смысл? Но эта аксиома требует выбрать что-то одно, пусть даже это будет безразличие. Она лишает нас возможности прибегнуть к оправданию «нельзя сравнивать яблоки с апельсинами». Аксиому соизмеримости можно интерпретировать как условие, что рациональный агент должен быть неравнодушным и предпочитать одни вещи другим. Нерациональные сущности вроде камней и овощей этому условию не удовлетворяют.
Вторая аксиома, аксиома транзитивности, уже интереснее. Сравнивая варианты попарно и отдавая предпочтение А перед В и В перед С, вы обязаны отдавать предпочтение А перед С. Легко увидеть, почему это требование не подлежит обсуждению: из любого, кто его нарушает, деньги можно выкачивать бесконечно. Допустим, смартфон Apple нравится вам больше, чем Samsung, но вы вынуждены ходить с Samsung Galaxу. Тогда вы согласитесь на мое предложение доплатить 100 долларов и обменять ваш гэлакси на элегантный айфон. Предположим, Google Pixel нравится вам даже больше айфона. Великолепно! Вы с радостью обменяете свой медленный айфон на мощный пиксель с доплатой, скажем, 100 долларов. И допустим, вы предпочитаете гэлакси пикселю — это нетранзитивность. Вы наверняка догадываетесь, к чему я веду. С доплатой в 100 долларов я продаю вам гэлакси. Вуаля: вы оказались в исходной точке, обеднев на 300 долларов, и готовы к следующему раунду обдираловки. Что бы вы ни думали о рациональности, это явно не она.
Третья аксиома — аксиома законченности. Учитывая, что бог играет с нами в кости и все такое, выбор наш не всегда однозначен — не так прост, как выбор сорта мороженого. Часто нам приходится выбирать между исходами, которые могут случиться с той или иной вероятностью — как при покупке лотерейного билета. Аксиома законченности гласит: если субъект, принимающий решения, способен выбирать между А и В, он может также учесть в своих размышлениях и лотерею, которая с вероятностью р вознаградит его призом А, а с дополняющей вероятностью 1-
В рамках теории рационального выбора исход рискованного выбора предсказать невозможно, однако вероятности определены — как в казино. Это
Есть… известные неизвестные — вещи, о которых мы знаем, что мы их не знаем. Но еще есть неизвестные неизвестные — это вещи, о которых мы не знаем, что мы их не знаем.
Теория рационального выбора объясняет, как принимать решения с известными неизвестными — рискуя, но не обязательно в условиях неопределенности.
Четвертую аксиому я назову аксиомой консолидации[249]. Жизнь не просто подсовывает нам лотерейные билеты — она подсовывает нам билеты, выигрыш по которым может оказаться еще одной лотереей. Если непредсказуемое первое свидание пройдет хорошо, может состояться и второе, которое принесет с собой новый набор рисков. Аксиома консолидации утверждает: столкнувшись с серией ситуаций рискованного выбора, субъект, принимающий решение, вычисляет общий риск согласно законам вероятности, изложенным в главе 4. Если первый лотерейный билет может выиграть с вероятностью один к десяти, а призом будет второй билет с вероятностью выиграть один к пяти, выбирающий сочтет его таким же желанным, как и билет, вероятность выигрыша по которому составляет один к пятидесяти. (Мы не учитываем дополнительное удовольствие от второй возможности посмотреть на подпрыгивающие шарики с номерами или соскрести с билетика краску.) Этот критерий рациональности кажется достаточно очевидным. Подобно ограничению скорости или всемирному тяготению, теория вероятности — не просто хорошая идея. Это закон.