Зачем я так и сяк кручу понятие условной вероятности, объясняя его то словами, то логическими функциями, то математическими формулами, то диаграммой Венна? Потому что условная вероятность — источник стольких ошибок, что еще одно объяснение лишним не будет[197].

Если вы мне не верите, подумайте об Уайтах, еще одной семье с двумя детьми. Как минимум один из детей — девочка. Какова вероятность, что оба ребенка девочки, то есть условная вероятность рождения двух девочек при условии, что одна девочка в семье точно есть, или, в математической записи, Р(1-й = девочка и 2-й = девочка | 1-й = девочка или 2-й = девочка)? Эту задачку верно решают столь немногие, что статистики называют ее парадоксом мальчика и девочки. Самый частый ответ 0,5; правильный — 0,33. Конкретное мышление в этом случае может привести к ошибке: люди представляют себе старшую девочку, понимают, что у нее может родиться либо брат, либо сестра, и решают, что сестра здесь — один шанс из двух. Они забывают, что эта известная нам девочка может оказаться младшей, а не старшей сестрой. Если правильно перечислять возможные варианты, мы получим один исход (девочка — девочка), деленный на три возможности (девочка — девочка, девочка — мальчик, мальчик — девочка), то есть 1/3. Или, по формуле условной вероятности, нужно разделить P(девочка и девочка), то есть 0,25, на P(девочка или девочка), то есть 0,75.

Парадокс мальчика и девочки — не просто математический трюк. Он порождается неспособностью нашего воображения пересчитать все возможные варианты и проявляется во множестве ипостасей, включая парадокс Монти Холла. Вот вам простой, но не менее точный эквивалент[198]. Уличные шулеры зарабатывают на жизнь, вовлекая прохожих в игру «Три карты в шляпе». Шулер показывает вам карту, красную с обеих сторон, карту, белую с обеих сторон, и карту, красную с одной стороны и белую с другой. Затем он кладет их в шляпу, встряхивает, вытаскивает одну, демонстрирует, что с лицевой стороны она, скажем, красная, и предлагает поспорить на деньги, что с изнанки она тоже красная (вы отдадите доллар, если изнанка красная, шулер отдаст доллар, если она белая). Это ловушка: шансы, что обратная сторона красная, составляют два к трем. Простаки мысленно пересчитывают карты, вместо того чтобы считать их стороны, забывая, что для красной с обеих сторон карты существует две возможности выпасть красной стороной вверх.

Кстати, помните парня, который пронес бомбу с собой в самолет? Он подсчитал общую вероятность того, что в самолете окажется две бомбы сразу. Но, притащив на борт свою собственную, он уже исключил из рассмотрения большую часть возможностей, представленных знаменателем. Вероятность, которая на самом деле должна его волновать, — условная вероятность присутствия на борту самолета двух бомб, при условии, что одна, его собственная, там уже есть (вероятность чего равна единице). А эта вероятность равна вероятности, что бомбу на борт пронесет кто-то еще, умноженной на 1 (конъюнкция его бомбы и чужой) и разделенной на 1 (вероятность его бомбы), что в итоге, естественно, равно вероятности того, что кто-то другой пронесет на борт бомбу, то есть как раз тому, с чего он и начинал. Эту шутку с успехом использовали в кинофильме «Мир по Гарпу» (The World According to Garp, 1982). Гарп приценивается к дому, когда в здание врезается легкомоторный самолет. Гарп говорит: «Мы его берем. Шансы, что в него врежется еще один самолет, астрономически малы»[199].

Забыть внести в базовую оценку вероятности поправку на заведомо имеющиеся особые обстоятельства — бушующую над вами грозу, бомбу, которую вы принесли с собой, — типичная ошибка при вычислении вероятностей. В 1995 г. в ходе суда над известным футболистом О. Дж. Симпсоном, обвиненным в убийстве жены Николь, прокурор привлек внимание присяжных к тому факту, что Симпсон неоднократно избивал супругу. Адвокат, член нанятой Симпсоном «команды мечты», ответил на это, что очень немногие бьющие жен мужья убивают своих жен — примерно один из двух с половиной тысяч. Ошибку заметила профессор-филолог Элейн Скарри. Николь Симпсон была не просто женщиной, которую бил муж. Она была жертвой избиений, которой к тому же перерезали горло. Так что считать здесь нужно условную вероятность того, что некто убил свою жену при условии, что он ее избивал и она была в итоге убита. А эта вероятность составляет уже 8 из 9[200].

Еще одна распространенная ошибка при вычислении условной вероятности — спутать вероятность А при условии В с вероятностью В при условии А, что можно назвать статистическим эквивалентом подтверждения консеквента — перехода от если Р, то Q к если Q, то Р[201]. Помните ипохондрика Ирвина, который был уверен, что у него болезнь печени, потому что его симптомы идеально подходили под описание: никакого дискомфорта? Ирвин спутал вероятность отсутствия симптомов при условии заболевания печени (высокую) с вероятностью заболевания печени при условии отсутствия симптомов (низкую). Загвоздка тут в том, что вероятность заболевания печени (ее базовая оценка) низка, а вероятность отсутствия дискомфорта высока.

Если базовые оценки различаются, условную вероятность нельзя переворачивать наоборот. Возьмем пример из жизни — открытие, что треть всех несчастных случаев со смертельным исходом случается дома, которому мы обязаны заголовком «Наше жилье — опасное место». Проблема в том, что дом — именно та точка, где мы проводим большую часть времени, так что, хотя жилье не является каким-то особенно опасным местом, там происходит масса несчастных случаев — просто потому, что там с нами вообще много всякого происходит. Автор заголовка спутал вероятность нахождения человека дома при условии несчастного случая со смертельным исходом (собранную статистику) с вероятностью несчастного случая со смертельным исходом при условии, что человек находится дома, которая на самом деле и интересует читателей. Ошибка становится интуитивно понятной, стоит только взглянуть на диаграмму, где относительные размеры кругов отражают разницу их базовых оценок (А — дни гибельных происшествий, В — дни, проведенные дома).

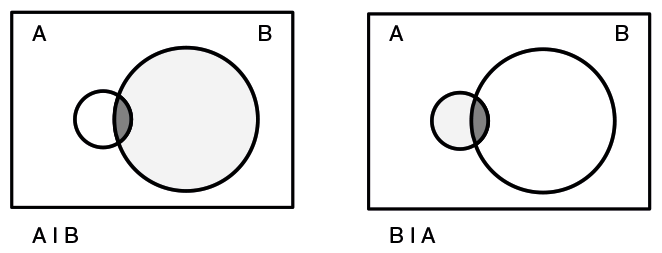
Левая диаграмма отражает вероятность А при условии В (вероятность несчастного случая со смертельным исходом при условии, что человек находится дома); это отношение площади темно-серой дольки (А и В) к площади большого светло-серого круга (В, быть дома); как видите, оно невелико. Правая диаграмма показывает вероятность В при условии А (вероятность находиться дома при условии несчастного случая со смертельным исходом); это отношение площади той же темно-серой дольки, но на этот раз уже к площади маленького светло-серого круга (несчастные случаи со смертельным исходом), и это отношение уже гораздо больше.

Причина, по которой условную вероятность так легко понять с точностью до наоборот, кроется в том, что язык не всегда позволяет однозначно уловить, к чему эта вероятность относится. «Вероятность наступления несчастного случая дома составляет 0,33» может означать и долю от всех несчастных случаев, и долю от времени, проведенного дома. Разница может потеряться, что повлечет за собой ложную оценку вероятностей. Большая часть велосипедистов, попадающих в дорожно-транспортные происшествия, — мальчики, и журналисты пишут: «Мальчики-велосипедисты подвергаются повышенному риску», что подразумевает, будто мальчики безответственнее девочек, хотя на самом деле может оказаться, что они просто чаще катаются на велосипеде. Совершая ошибку, которую статистики называют ошибкой обвинителя, окружной прокурор заявляет: вероятность, что группа крови жертвы случайно совпадет с группой крови, обнаруженной на одежде подсудимого, составляет 3 % — и заключает, что подсудимый виновен с вероятностью 97 %. Он спутал (и надеется, что присяжные спутают) вероятность совпадения группы крови при условии невиновности подсудимого с вероятностью невиновности подсудимого при условии совпадения группы крови[202]. Как вычислить эту вероятность правильно — тема следующей главы, посвященной байесовскому мышлению.

Двусмысленность условных вероятностей может спровоцировать скандал. В 2019 г. пара социологов произвела фурор, опубликовав исследование в престижном журнале Proceedings of the National Academy of Sciences, где они, опровергая всеобщую убежденность в расовой предвзятости полиции, утверждали, опираясь на статистику вроде той, что я упоминал выше, будто полицейские чаще убивают белых, а не черных американцев. Их оппоненты указали, что этот вывод относится к вероятности, что некто — черный при условии, что его застрелила полиция, которая действительно ниже, чем соответствующая вероятность для белого человека, но только потому, что белых в стране больше, чем черных, — то есть у этих вероятностей разные базовые оценки. Если полиция действительно расово предубеждена, эта предрасположенность проявилась бы как повышенная вероятность того, что некто будет застрелен полицейским при условии, что он — черный, и согласно имеющимся данным эта вероятность действительно выше. Первоначально авторы возразили, что не вполне понятно, какие базовые оценки тут следует использовать — долю черных в популяции или долю черных среди тех, кого останавливает полиция, но затем осознали, до какой степени напортачили с формулировками вероятностей, и официально отозвали статью[203].

А что там, кстати, с папой-инопланетянином? Вот что получается, когда путаешь вероятность, что некто — папа римский при условии, что он — землянин, с вероятностью, что некто — землянин при условии, что он — папа римский[204].

Априорная и апостериорная вероятность

Мужчина примеряет сшитый на заказ костюм и говорит портному: «Правый рукав надо бы подобрать». Портной отвечает: «А ну-ка, согните руку в локте. Видите, рукав подтянулся». Клиент возражает: «Но если я сгибаю руку, то воротник сзади оттопыривается». Портной говорит: «Ну и что? Вытяните шею и выпрямите спину. Вот, смотрите, как хорошо». Мужчина продолжает: «Но теперь левое плечо на 10 сантиметров ниже правого!» Портной не уступает: «Не беда, вы просто немного наклонитесь влево». Мужчина выходит из ателье в новом костюме: правый локоть оттопырен, подбородок задран, скрючился и еле ковыляет. Навстречу ему идут двое прохожих. «Видишь того инвалида? — шепчет один. — Вот бедолага». Второй отвечает: «Да, но у его портного золотые руки: костюм сидит как влитой!»

Этот анекдот знакомит нас с еще одним типом заблуждений в области теории вероятности: неумением отличить априорные суждения от апостериорных. Эту ошибку иногда называют ошибкой техасского стрелка — в честь снайпера, который сначала выпускает пулю в стену сарая, а затем рисует вокруг дырки мишень. При вычислении вероятностей очень важно, чтобы знаменатель дроби — количество всех возможностей для того, чтобы данное событие произошло, — подсчитывался независимо от числителя, то есть количества интересующих нас событий. В основе ошибки техасского стрелка лежит предвзятость подтверждения, которую мы обсуждали в главе 1: ожидая чего-то определенного, мы ищем подтверждающие примеры и игнорируем опровергающие. Собрав сбывшиеся предсказания пророка, но не разделив их на общее число предсказаний — как верных, так и неверных, можно получить какую угодно вероятность. Как еще в 1620 г. заметил Фрэнсис Бэкон, таково происхождение почти всех суеверий — астрологии, вещих сновидений, предсказаний оракулов или божественных откровений.

Или финансовых прогнозов. Бессовестный инвестиционный консультант со списком контактов в сто тысяч адресов отправляет одной половине потенциальных клиентов информационное письмо с прогнозом роста котировок, а другой — письмо с прогнозом их падения. В конце каждого квартала он вычеркивает людей, которым отправил несбывшийся прогноз, и заново проворачивает тот же трюк с оставшимися. Через два года он заключает контракты с 1562 адресатами, восхищенными его способностью предвидеть движения рынка на протяжении восьми кварталов подряд[205].

Хотя подобные махинации незаконны, если мошенник понимает, что делает, бессознательное их осуществление — плоть и кровь финансовой индустрии. Выгодные предложения расхватываются трейдерами в мгновение ока, поэтому очень немногие финансовые аналитики способны заработать больше примитивной сбалансированной корзины ценных бумаг. Исключением стал Билл Миллер, в 2006 г. объявленный журналом CNN Money «величайшим инвестиционным управляющим современности», поскольку ежегодные показатели доходности его фонда на протяжении 15 лет подряд превышали показатели фондового индекса S&P 500. Впечатляет, не правда ли? Казалось бы, если в каждом отдельно взятом году аналитик с равной вероятностью может либо обыграть индекс, либо уступить ему, шанс, что это произойдет по чистой случайности, равен 1 к 32768 (2¹⁵). Но удивительную полосу везения Миллера обнаружили только после того, как она случилась. Как заметил физик Леонард Млодинов в книге «(Не)совершенная случайность. Как случай управляет нашей жизнью» (The Drunkard’s Walk: How Randomness Rules Our Lives, 2008), в стране примерно шесть тысяч инвестиционных управляющих, а паевые инвестиционные фонды современного типа существуют уже около сорока лет. Шанс, что какой-нибудь управляющий в какой-то период этого сорокалетнего интервала на протяжении пятнадцати лет будет обыгрывать индекс, вовсе не низок — он составляет 3 из 4. CNN Money лучше было бы написать: «Ожидаемая пятнадцатилетняя полоса везения наконец зафиксирована: счастливчика зовут Билл Миллер». И конечно же, в конце концов удача Миллеру изменила, так что в следующие два года рынок «стер его в порошок»[206].

Помимо предвзятости подтверждения, основной источник ошибок, связанных с апостериорной вероятностью, — наша неспособность осознать, до какой степени окружающий мир изобилует возможностями для разного рода совпадений. Если начать искать совпадения постфактум, они почти наверняка найдутся. В одной из колонок, написанных для журнала Scientific American, классик математических развлечений Мартин Гарднер спрашивал:

Обратите ли вы внимание, что номерной знак впереди идущего автомобиля, прочтенный задом наперед, совпадает с номером вашего телефона? Кто, кроме нумеролога или логоманьяка подметит, что буквы U, S, A симметрично расположены посредине слова Louisiana или на конце фамилии Sousa, принадлежащей автору американских патриотических маршей? Каким чудаком надо быть, чтобы подметить, что Ньютон появился на свет в год смерти Галилея или что Бобби Фишер (Fischer) родился под знаком Рыб (Fish)[207].

Однако такие нумерологи и чудаки существуют, и на их апостериорной приметливости построено немало затейливых теорий. Типичнейшее явление, не нуждающееся в объяснениях, а именно обилие в нашем мире совпадений, психоаналитик Карл Густав Юнг объяснял вмешательством таинственной силы под названием «синхроничность».

Когда я был ребенком, то, что теперь называют мемами, распространялось посредством комиксов и популярных журналов. Одно время у всех на слуху был перечень невероятных совпадений в жизненных обстоятельствах Авраама Линкольна и Джона Ф. Кеннеди. И честный Эйб, и JFK были избраны в Конгресс в 46-м году, а на пост президента — в 60-м. Оба были убиты выстрелом в голову в пятницу в присутствии жены. У Линкольна был секретарь по фамилии Кеннеди; у Кеннеди был секретарь по фамилии Линкольн. Обоих сменил на посту Джонсон, рожденный в 8-м году. Их убийцы были 39-го года рождения, имена их состояли из трех слов — и пятнадцати букв. Джон Уилкс Бут (John Wilkes Booth) сбежал из театра и был пойман на складе. Ли Харви Освальд (Lee Harvey Oswald) сбежал со склада и был пойман в театре. О чем же нам говорят эти странные параллели? При всем уважении к доктору Юнгу, ровным счетом ни о чем, кроме того, что совпадения случаются чаще, чем готовы признать наши статистически неподкованные мозги. И это я еще не упомянул о том, что, обретя популярность, сверхъестественные совпадения приукрашиваются (у Линкольна не было секретаря по фамилии Кеннеди), а досадные несовпадения (вроде того, что Линкольн и Кеннеди родились и умерли в разные дни, месяцы и годы) игнорируются.