Удивительная математика Пакстона предполагает, что голоса, накапливающиеся по ходу подсчета, статистически независимы, словно ряд бросков игральной кости. Но горожане голосуют не так, как жители пригородов, которые, в свою очередь, голосуют не так, как сельские жители, а избиратели, голосовавшие лично, голосуют не так, как те, кто голосовал по почте (особенно на выборах 2020 г., когда Трамп громогласно призывал своих сторонников не голосовать по почте). Решения избирателей каждой из этих групп не являются независимыми, а базовые оценки отличаются от группы к группе. Кроме того, так как результаты по избирательным участкам обнародуют сразу по окончании подсчета, а голоса, поданные по почте, прибавляются к ним позже, по мере поступления данных, промежуточная сумма голосов в пользу каждого из кандидатов то растет, то падает, и экстраполировать окончательные итоги на основании промежуточных не представляется возможным. Абсурдность обвинений достигла четвертой степени, когда Пакстон перемножил выдуманные вероятности по каждому из четырех штатов, итоги выборов в которых также не являются независимыми: то, что влияло на мнение избирателей Мичигана, влияло, скорее всего, и на избирателей Висконсина[192].

Статистическая независимость связана с понятием причинности: если одно событие влияет на другое, они не являются статистически независимыми (хотя, как мы еще увидим, обратное неверно: события, не связанные отношениями причины и следствия, могут оказаться зависимыми статистически). Вот почему ошибка игрока — это ошибка. Одно вращение колеса рулетки никак не влияет на другое, поэтому азартный человек, рассчитывающий, что череда «черного» вымостит дорожку «красному», проиграется до нитки: вероятность выпадения «красного» всегда чуть меньше 0,5 (потому что есть еще зеленые ячейки 0 и 00). Заметьте, что ошибаться относительно статистической независимости можно и так и эдак: можно ошибочно предполагать как независимость (закон Мидоу), так и зависимость событий (ошибка игрока).

Зависят события друг от друга или нет, очевидно не всегда. Одна из известнейших попыток приложить науку о когнитивных искажениях к решению житейских загадок — анализ феномена «горячей руки» в баскетболе, произведенный Тверски в сотрудничестве с социальным психологом Томасом Гиловичем[193]. Любому болельщику известно, что время от времени баскетболист может быть «в ударе», «на кураже» или «на драйве»; тут сразу вспоминается «серийный бомбардир» Винни Джонсон, который в 1980-е гг. играл на позиции атакующего защитника в Detroit Pistons и заслужил прозвище «Микроволновка», потому что умел молниеносно «разогреть» атаку. Вопреки мнению болельщиков, тренеров, игроков и спортивных журналистов, Тверски и Гилович пришли к выводу, что «горячая рука» — иллюзия, своего рода ошибка игрока. Проанализированные ими данные свидетельствовали, что результат каждого броска статистически независим от предшествующей череды попыток забросить мяч в кольцо.

Однако, не изучив данные, неверно отрицать реальность феномена «горячей руки» по примеру ошибки игрока просто из-за отсутствия причинно-следственной связи. В отличие от колеса рулетки, тело и мозг спортсмена обладают памятью, и думать, что всплеск энергии или уверенности в себе может длиться несколько минут подряд, — отнюдь не суеверие. Так что другие статистики не нанесли удара по научному мировоззрению, когда покопались в данных еще раз и пришли к выводу, что светила науки ошиблись, а фанаты были правы: феномен «горячей руки» в баскетболе существует. Экономисты Джошуа Миллер и Адам Санхурхо показали: если выделить из последовательности данных череду попаданий или промахов, результат следующей за этой чередой попытки не является статистически от нее независимым. Дело в том, что, если попытка оказалась удачной, она продолжает счастливую полосу, и ее могли изначально к ней причислить. Любая попытка, которая выделяется в ряду только потому, что случилась следом за счастливой полосой, скорее будет неудачной — такой, которую невозможно определить как часть полосы везения. Это перечеркивает вычисления, основанные на предположении о случайности событий, что, в свою очередь, опровергает заключение, будто баскетболисты так же непоследовательны, как колесо рулетки[194].

Ошибка ошибки «горячей руки» преподает нам три урока. Во-первых, события могут быть статистически зависимыми не только если одно из них является причиной другого, но и если оно влияет на то, какое событие выбирается для сравнения. Во-вторых, ошибка игрока может возникать благодаря отчасти рациональному свойству восприятия: когда мы ищем цепочки идентичных исходов в длинном ряду событий, череда определенной длины действительно с большей вероятностью прервется, чем продолжится. В-третьих, вероятность действительно бывает глубоко неинтуитивна: даже знатоки способны наделать ошибок в вычислениях.

Теперь давайте рассмотрим вероятность дизъюнкции событий, Р(А или В). Она равна сумме вероятностей А и В по отдельности минус вероятность (А и В). Если у Браунов двое детей, то вероятность, что хотя бы один из них — девочка (то есть что первый ребенок — девочка или второй ребенок — девочка), равна 0,5 + 0,5–0,25, то есть 0,75. Тот же результат мы получим, перечислив комбинации: три варианта (мальчик — девочка, девочка — девочка, девочка — мальчик) из четырех (мальчик — девочка, мальчик — мальчик, девочка — мальчик, девочка — девочка). Можно еще подсчитать частоту: на большой выборке семей с двумя детьми вы обнаружите, что в 75 % из них растет хотя бы одна девочка.

Формула вероятности разделительного высказывания подсказывает, где ошибся телеметеоролог, заявивший, что в выходные обязательно прольется дождь, потому что и в субботу, и в воскресенье вероятность дождя составляет 50 %: сложив две вероятности, он дважды посчитал все те выходные, в которые дождь будет идти два дня подряд, то есть забыл вычесть конъюнкцию, равную 0,25. Он применил правило, которое работает для исключающего или (XOR), а именно А или В, но не то и другое одновременно. Вычисляя дизъюнкцию взаимно исключающих событий, складывать их вероятности можно: их сумма всегда будет равна единице. Вероятность, что ребенок окажется либо мальчиком (0,5), либо девочкой (0,5), равна сумме двух этих вероятностей, то есть 1, других вариантов нет (для наглядности я придерживаюсь здесь идеи гендерной бинарности и не учитываю интерсекс-детей). Забыв об этой разнице и спутав пересекающиеся события со взаимно исключающими, можно получить умопомрачительные результаты. Представьте, что метеоролог предсказывает 50 %-ную вероятность дождя в субботу, в воскресенье и в понедельник и заключает, что на протяжении длинных выходных дождь прольется с вероятностью 1,5.

Вероятность дополнения события, а именно P(не-А) (А не случится), равна 1 минус вероятность P(А) (А случится). Это удобно, когда нам нужно оценить вероятность «как минимум одного» события. Помните Браунов с их то ли двумя, то ли одной дочкой? Как минимум одна дочка — это то же самое, что не все дети — сыновья, и вместо вычисления дизъюнкции (первый ребенок девочка или второй ребенок девочка) мы можем вычислить дополнение конъюнкции: 1 минус вероятность рождения двух мальчиков (которая равна 0,25), и получить в итоге 0,75. В случае двух событий неважно, какой из формул пользоваться. Но если нам нужно посчитать вероятность как минимум одного А в крупном наборе событий, правило дизъюнкции потребует кропотливого сложения и вычитания массы комбинаций. Гораздо легче вычислить вероятность «не все не-А», то есть 1 минус произведение всех вероятностей А.

Предположим, например, что каждый год характеризуется 10 %-ной вероятностью начала войны. Каковы шансы, что на протяжении десяти лет разразится хотя бы одна война? (Давайте примем, что войны — независимые, а не контагиозные события, какими они, похоже, являются.)[195] Вместо того чтобы прибавлять к вероятности войны в год № 1 вероятность войны в год № 2 и вычитать из этой суммы вероятность того, что война начнется и в год № 1, и в год № 2 и так далее для всех возможных комбинаций, мы можем просто вычислить шансы, что никакой войны за десять лет не вспыхнет, и вычесть их из единицы. Вероятность десяти мирных лет равна вероятности, что война не начнется в каждый отдельный год из этих десяти, а именно 0,9, умноженному само на себя десять раз (0,9 × 0,9 × …0,9, или 0,9¹⁰, что равно 0,35). Вычтя 0,35 из единицы, получаем 0,65.

И наконец, мы добрались до условной вероятности: вероятности А при условии, что В верно, что записывается как Р(А|В). Смысл этого понятия прост: это всего лишь вероятность то в связке если-то. Рассчитать ее тоже не сложно: это вероятность (А и В), деленная на вероятность В. Тем не менее условная вероятность — источник бесчисленных конфузов, просчетов и промахов при оценке вероятности, начиная с ошибки, которую совершает безнадежный идиот из приведенного ниже комикса XKCD[196]. Он спутал простую вероятность, или базовую оценку риска гибели от удара молнии, Р(убит молнией) с условной вероятностью погибнуть от удара молнии при условии, что ты находишься на улице в сильную грозу: Р(убит молнией | на улице в сильную грозу).

Хотя расчет условной вероятности прост, интуитивно его не ухватишь, пока не представишь себе ситуацию и не конкретизируешь ее (как всегда). Взгляните на диаграммы Венна, где площадь областей на листе соотносится с числом исходов. Прямоугольник, площадь которого принимается за единицу, соответствует всей совокупности возможных исходов. Круг А заключает в себе все события А, и на рисунке слева вверху видно, что вероятность А равна соотношению площади круга А (выделенного темным цветом) к площади светло-серого прямоугольника — другими словами, числу случившихся событий, деленному на число его возможностей случиться. Рисунок справа вверху иллюстрирует вероятность (А или В) — это вся темная зона, то есть площадь А плюс площадь В минус та долька, где множества А и В пересекаются — (А и В), а иначе мы посчитаем ее дважды. Эта же долька, Р (А и В), выделена темным цветом на нижнем левом рисунке.

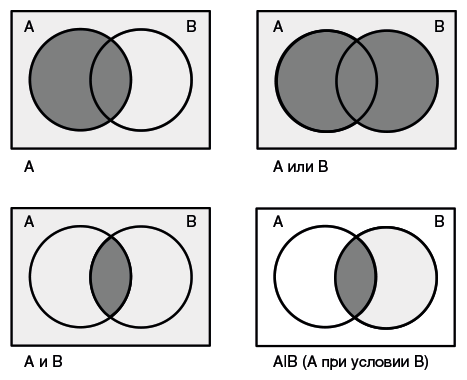
Рисунок, помещенный внизу справа, раскрывает смысл понятия условной вероятности. Здесь видно, что при таком расчете мы должны игнорировать пространство всех теоретически возможных исходов (белого цвета) и сосредоточить внимание только на исходах, когда случилось В, то есть на светло-сером круге B. Давайте попробуем вычислить, какую долю от них составляют такие, где случилось и А тоже, — это площадь дольки (А и В), деленная на площадь круга В. Какая доля случаев появления человека на улице в сильную грозу (В) завершилась гибелью от удара молнии (А и В)? Вот почему мы вычисляем условную вероятность Р(А|В) путем деления вероятности конъюнкции Р(А и В) на базовую оценку Р(В).

Вот пример: у Греев двое детей. Старшая — девочка. Какова при этом вероятность, что дочек у Греев две? Давайте переведем вопрос в термины условной вероятности, то есть вероятности, что первый ребенок — девочка и второй ребенок — девочка, при условии, что первый ребенок — девочка. Это можно записать так: Р (1-й = девочка и 2-й = девочка | 1-й = девочка). Следуя формуле, нам нужно разделить конъюнкцию, которая, как мы уже подсчитали, равна 0,25, на вероятность появления на свет первой девочки, которая составляет 0,5; в результате мы получим 0,5. Или, если рассуждать в классической парадигме, разделив один исход (девочка — девочка) на две возможности (девочка — девочка и девочка — мальчик), получим 1/2.

Условная вероятность помогает уточнить понятие статистической независимости, объяснение которого я не довел до конца. Теперь мы можем дать такое определение: А и В независимы, если для всех В вероятность А при условии В равна вероятности А (и то же самое верно для В). Помните ошибку перемножения вероятностей при вычислении конъюнкции зависимых событий? Хотите узнать правильное решение? Легко: вероятность конъюнкции P(А и В), если они не являются независимыми, равна вероятности А, умноженной на вероятность В при условии А, то есть Р(А) × Р(В|А).