Недавно мы с коллегой поспорили о том, какое послание должен адресовать миру наш университет по вопросу глобального потепления. По мнению моего оппонента, нам просто нужно убеждать людей, что сокращение объема производимых ими парниковых газов отвечает их личным интересам, поскольку перегретая планета — это наводнения, ураганы, лесные пожары и другие бедствия, от которых они же и пострадают. Я же говорил, что разумное потребление отнюдь не отвечает личным интересам отдельного человека, поскольку никакая жертва с его стороны не предотвратит изменений климата; при этом сознательная гражданка будет потеть летом, дрожать от холода зимой и под проливным дождем ждать автобуса, в то время как ее несознательные соседи не перестанут наслаждаться комфортной температурой и сухим салоном своего автомобиля. Любой из нас выиграет лишь в том случае, если свой углеродный след минимизируют все, а выгодным для каждого в отдельности это будет, только если сделать чистую энергию дешевле (благодаря новым технологиям), а грязную — дороже (за счет тарифов на выбросы углерода). Мой коллега говорил вполне разумную вещь: с одной стороны, разрушать планету — нерационально. Но мне никак не удавалось убедить его, что, с другой стороны, это, увы, абсолютно рационально.

Тогда-то я и понял, что этот прекрасный специалист упускает из виду принципиально важную концепцию — теорию игр, подсказывающую, как делать рациональный выбор, когда размер твоего вознаграждения зависит от рационального выбора другого человека.

С теорией игр мир познакомили фон Нейман и Моргенштерн — в той же самой книге, где объясняли, что такое ожидаемая полезность и рациональный выбор[310]. Но в отличие от дилемм, в рамках которых мы испытываем судьбу, играя против безмозглого колеса фортуны, и где, как оказалось, наилучшие стратегии в целом интуитивны, теория игр имеет дело с дилеммами, сталкивающими нас с равно хитроумными игроками, и тут уж исходы выворачивают наши интуитивные догадки наизнанку и переворачивают их с ног на голову. Жизненные игры порой не оставляют рациональному агенту выбора: он вынужден совершать поступки, от которых пострадает и он сам, и все остальные, вести себя беспорядочно, капризно или неуправляемо, лелеять симпатии и копить обиды, с готовностью переносить наказания и подвергаться взысканиям или вовсе отказываться участвовать в игре. Теория игр проливает свет на парадоксальную рациональность, стоящую за многими странностями общественной и политической жизни, и, как станет понятно в одной из последующих глав, помогает ответить на центральный вопрос этой книги: как наш рациональный вид может быть таким нерациональным?

Игра с нулевой суммой: камень, ножницы, бумага

Классическая дилемма теории игр, где четко видно, как выгодность выбора одного участника зависит от выбора другого, — игра «Камень, ножницы, бумага»[311]. Два игрока одновременно показывают какой-то из жестов: либо два пальца (ножницы), либо открытую ладонь (бумага), либо кулак (камень), — а победитель определяется согласно правилу «ножницы режут бумагу, бумага обертывает камень, камень тупит ножницы». Правила можно представить в виде таблицы: выборы первого игрока, Аманды, записаны в строках, выборы второго игрока, Брэда, — в столбцах, а исходы — в ячейках: для Аманды в нижнем левом углу, для Брэда в верхнем правом. Давайте присвоим исходам численные значения: 1 — победа, –1 — проигрыш, 0 — ничья.

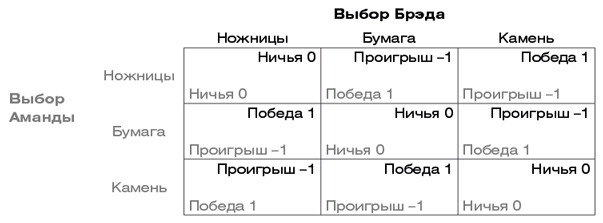
Сумма выигрышей Аманды и Брэда равна нулю в каждой ячейке, отсюда и термин, который проник из теории игр в разговорную речь: игра с нулевой суммой. Победа Аманды — это поражение Брэда, и наоборот. Игроки находятся в состоянии непримиримого конфликта и дерутся за один и тот же кусок пирога.

Какой ход (строку) должна выбрать Аманда? Основной алгоритм в теории игр (да и в жизни тоже) — взглянуть на ситуацию глазами другого игрока. Аманда должна изучить выборы Брэда (столбцы) один за другим. Проследим слева направо: если Брэд выбирает ножницы, Аманде нужно выбрать камень. Если он выбирает бумагу, ей нужно выбрать ножницы. Если он выбирает камень, ей нужно выбрать бумагу. У Аманды нет никакого «предпочтительного» выбора — наилучшего вне зависимости от того, что сделает Брэд; а Аманда, естественно, понятия не имеет, что он собирается делать.

Однако это еще не значит, что Аманда должна выбрать какой-то один ход, бумагу например, и упрямо его придерживаться. Если она так поступит, Брэд это заметит, станет все время показывать ножницы и будет раз за разом одерживать верх. Более того, даже если Аманда станет выбирать бумагу всего лишь немного чаще, чем другие варианты (скажем, в 40 % случаев, а каждый из двух других — в 30 %), Брэд может сделать ставку на ножницы и побеждать четыре раза из семи. Наилучшая стратегия для Аманды — превратиться в человека-рулетку и выбирать ходы случайным образом с одной и той же вероятностью, исключая любой уклон, крен, дрейф или шаг в сторону от идеального разбиения 1/3–1/3–1/3.

Поскольку приведенная выше таблица симметрична относительно диагонали, Брэду нужно вести себя точно так же. Когда он, строка за строкой, обдумывает варианты действий Аманды, у него нет оснований предпочесть один из своих ходов двум другим, и, следовательно, он вынужден придерживаться той же «смешанной» стратегии, разыгрывая каждый вариант с вероятностью 1/3. Если же Брэд от нее отступит, Аманда изменит свою линию поведения, чтобы этим воспользоваться, и наоборот. Игроки зависли в равновесии Нэша, названном по имени математика Джона Нэша, героя фильма «Игры разума» (A Beautiful Mind, 2001). Каждый из них следует наилучшей стратегии с учетом наилучшей стратегии оппонента; любое одностороннее изменение ухудшит положение игрока.

Открытие, что в некоторых ситуациях рациональный агент должен вести себя сверхчеловечески неупорядоченно, — лишь один из выводов теории игр, который кажется абсурдным, пока не осознаешь, что в жизни таких ситуаций полно. Равновесие игры «Камень, ножницы, бумага» называют коллизией угадывания, и ее нередко можно наблюдать в таких видах спорта, как теннис, бейсбол, хоккей или футбол. Футболист, бьющий пенальти, может послать мяч либо в правый угол ворот, либо в левый, а вратарь может защитить либо левый угол, либо правый; в такой ситуации непредсказуемость — первостепенное достоинство. Блеф в покере и внезапные атаки в военной стратегии — те же коллизии угадывания. Даже если действие выбирается не в буквальном смысле случайно (скорее всего, в 1944 г. союзники не подбрасывали монетку, чтобы решить, где высаживаться — в Нормандии или в районе Кале), игрок должен сделать каменное лицо, чтобы не выдать себя ни словом, ни взглядом и заставить оппонентов считать его выбор случайным. Философы Лиам Клегг и Дэниел Деннет выдвинули идею, что поведение людей непредсказуемо по самой своей природе не только из-за случайного нейронного шума в мозге; это еще и адаптация, которая мешает соперникам читать нас, как открытую книгу[312].

Игра с ненулевой суммой: дилемма добровольца

Рациональные агенты попадают в коллизию угадывания не только в играх с нулевой суммой, но и в ситуациях, когда их интересы отчасти совпадают. Пример — дилемма добровольца, которую прекрасно иллюстрирует средневековая басня «Колокольчик для кошки». Мышь предлагает товаркам повесить колокольчик на шею спящей кошки, чтобы звон оповещал о приближении хищника. Вопрос, конечно же, в том, кто именно повесит колокольчик, рискуя разбудить кошку и быть съеденным. Люди тоже сталкиваются с похожими дилеммами: например, кто из пассажиров схлестнется с угонщиком самолета, кто из прохожих поможет человеку в беде и кто из офисных работников почистит кофеварку на общей кухне[313]. Каждый хочет, чтобы кто-нибудь это сделал, и каждый предпочел бы, чтобы это был не он. Если обозначить издержки и выгоды числами (0 — худшее, что может случиться), мы получим таблицу, приведенную ниже. (Точнее, это должен быть гиперкуб с числом измерений, равным числу игроков, но я свернул всех, кроме «себя», в один слой.)