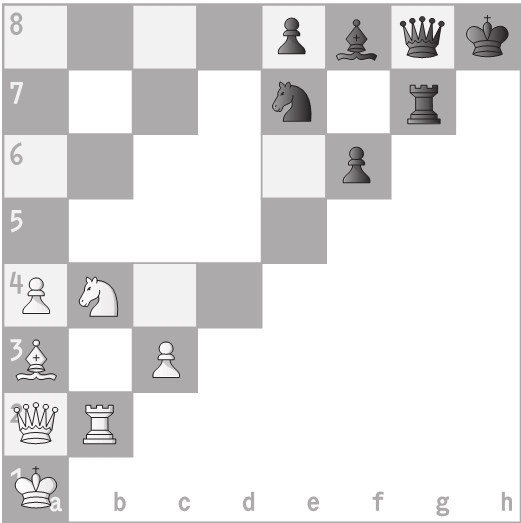
▒ Без взятия белые пешки ходят вверх, черные – влево. Со взятием белые пешки ходят влево-вверх или вправо-вверх, черные пешки – влево-вниз или влево-вверх. Белые пешки достигают верхнего края доски, черные – левого.

▒ Здесь нет взятия на проходе, рокировки или прыжка пешки через одно поле.

▒ Шахматные фигуры не могут ходить на 37 закрытых квадратов или перепрыгивать через них. Конь также не может ходить на 37 закрытых квадратов, но «перепрыгивать» может через что угодно.

Эти шахматы названы 1,58‐мерными, потому что 27 открытых квадратов выбраны в соответствии с закономерностью, по которой строится треугольник Серпинского: сначала вы берете один открытый квадрат, а затем удваиваете ширину, дублируя фигуру предыдущего шага в верхний левый, верхний правый и нижний левый углы, а нижний правый угол оставляете нетронутым. Поскольку в одномерной структуре удвоение ширины увеличивает пространство в 2 раза, в двумерной – в 4 раза (4 = 22), а в трехмерной – в 8 раз (8 = 23), здесь удвоение ширины увеличивает пространство в 3 раза (3 = 21,58496), отсюда и «1,58‐мерность».

Игра существенно проще и «податливее», чем полноценные шахматы, и она дает возможность с интересом пронаблюдать, как в пространствах меньшей размерности защита становится намного проще нападения. Обратите внимание, что относительная ценность разных фигур здесь может измениться и появятся новые виды концовок (например, можно поставить мат одним слоном).

ТРЕХМЕРНЫЕ КРЕСТИКИ-НОЛИКИ

Цель игры – выстроить прямую линию из четырех крестиков или ноликов вдоль оси или по диагонали, в том числе между плоскостями. Например, в этой конфигурации Х выигрывает.

МОДУЛЯРНЫЕ КРЕСТИКИ-НОЛИКИ

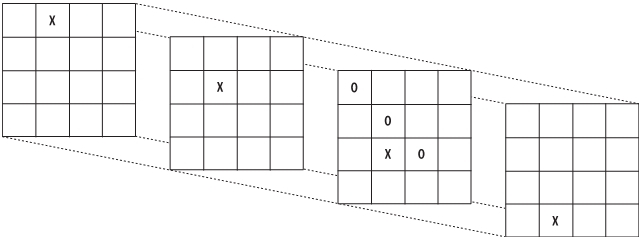
Здесь мы возвращаемся к двум измерениям, но теперь линии могут перескакивать.

Х выигрывает

Обратите внимание, что допускаются диагональные линии с любым наклоном: главное – чтобы они проходили через все четыре точки. Например, вполне возможны линии с наклоном +/– 2 и +/– 1/2:

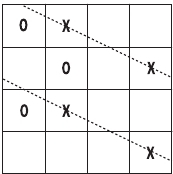
Математически доску можно интерпретировать как двумерное векторное пространство над целыми числами по модулю 4, и цель заключается в том, чтобы заполнить линию, проходящую через четыре точки над этим пространством. Обратите внимание, что существует по крайней мере одна линия, проходящая через любые две точки.

КРЕСТИКИ-НОЛИКИ НА ДВОИЧНОМ ПОЛЕ С 4 ЭЛЕМЕНТАМИ

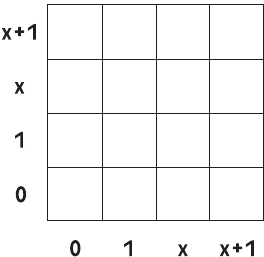
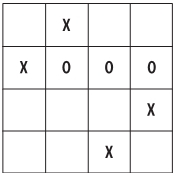
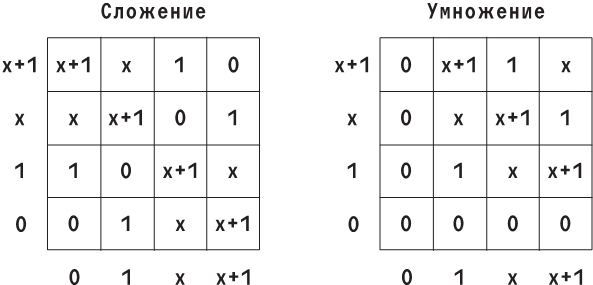
Здесь та же концепция, что и выше, за исключением того, что мы используем еще более жуткую математическую структуру – 4-элементное поле многочленов над Z2 по модулю x2 + x + 1. У этой структуры практически нет адекватной геометрической интерпретации, поэтому я просто приведу таблицы сложения и умножения.

Ну ладно, вот для удобства все возможные линии, за исключением горизонтальных и вертикальных (которые также допустимы).

Отсутствие геометрической интерпретации действительно усложняет игру. По сути, вам придется запомнить все двадцать выигрышных комбинаций – хотя заметьте, что в основном они представляют собой переносы и отражения одних и тех же четырех основных фигур (осевая линия; диагональная линия; диагональная линия, начинающаяся посередине; и эта странная штука, которая вообще не похожа на линию).

А ВОТ 1,77‐МЕРНЫЕ «ЧЕТЫРЕ В РЯД». РИСКНЕТЕ СЫГРАТЬ? МОДУЛЯРНЫЙ ПОКЕР

Каждому раздается по пять карт (здесь можно использовать любую разновидность покера с точки зрения того, как раздаются карты и имеют ли игроки право их менять). У карт будут следующие числовые значения: валет = 11, дама = 12, король = 0, туз = 1. Самой сильной считается та рука, которая содержит более длинную последовательность с любым повторяющимся интервалом между следующими друг за другом картами («колесо» здесь тоже допустимо).

Математически это можно представить так: рука сильнее, если игрок может найти такое выражение L(x) = mx + b, под которое у него найдутся карты для чисел L(0), L(1)…L(k) для наибольшего k.

Пример полной выигрышной комбинации из пяти карт. y = 4x + 5