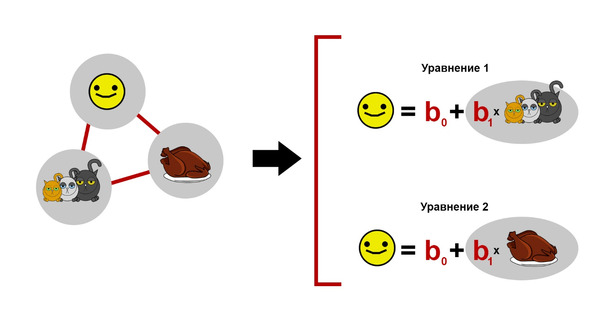
Как правило, эту проблему преодолевают тремя способами.

1. Исключают одну из коррелирующих переменных из анализа.

2. Предварительно проводят процедуру факторного анализа (о нем будет рассказано далее), заменяющего эти переменные одной искусственной, которая и будет включена в регрессию.

3. Проводят процедуру пошаговой регрессии. Такая регрессия постепенно включает в уравнение по одной переменной и сразу же после этого пересчитывает вклад всех остальных. В итоге если одна из коррелирующих переменных была выбрана в качестве фактора, вторая туда скорее всего не попадет.

Вторая проблема — проблема переобучения — заключается в том, что уравнение, полученное на одних котиках, может не работать на других. Она возникает из-за того, что в вашей выборке котиков могут быть закономерности, которые нехарактерны для котиков в целом. И зачастую они попадают в регрессионную модель.

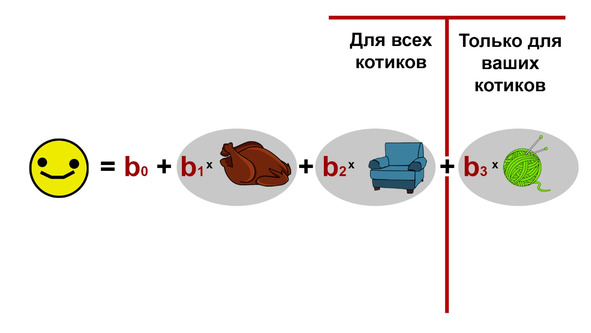
Для того чтобы предотвратить переобучение, используют критерий, который искусственно ограничивает количество факторов, включенных в уравнение (например критерий Акаике и Байесовский информационный критерий).

Глава 12.

Котиковые аналоги

или основы математического моделирования

В предыдущих разделах мы подробно рассмотрели метод регрессионного анализа, который позволяет построить уравнение, описывающее, как различные вещи влияют на настроение котиков. Подобные уравнения входят в группу объектов, называющихся математическими моделями.

Математическая модель — это своего рода аналог котика, который позволяет изучать его поведение без проведения реальных экспериментов. Как правило, это значительно удешевляет исследования.

Все математические модели делятся на функциональные и структурные. Функциональные модели, к которым, к слову, относится регрессионное уравнение, — описывают влияние внешних факторов на котиковое состояние. Например, известная нам модель котикового счастья.

Особенность такой модели в том, что мы подробно не рассматриваем состав этого счастья. Счастье для нас — некий целостный объект, целевая переменная, которая может меняться: прибывать или убывать. А вот структурные модели позволяют описать его компоненты: от удовлетворения базовых котиковых потребностей до котиковой самореализации.

Как правило, функциональные модели записываются с помощью уравнений. А вот структурные могут быть достаточно разнообразными: от таблиц до блок-схем.

Любая математическая модель строится в два этапа. На первом этапе мы прикидываем, какие факторы в принципе могут влиять на котиковое счастье или из каких компонентов оно может состоять. Этот этап называется также построением содержательной модели.

Второй этап включает в себя сбор реальных данных и их математическую обработку. Он называется построением формальной модели. Формальную модель уже можно использовать как аналог реального котика. Изменяя различные параметры этой модели, вы сможете понять, как функционирует котик, не прибегая к опытам над животными.

НЕМАЛОВАЖНО ЗНАТЬ!

Классификация математических моделей

Помимо деления на функциональные и структурные модели есть еще несколько классификаций, о которых полезно знать. В частности бывают модели статические и динамические. Первые описывают состояние котика в какой-то конкретный момент. Вторые же концентрируются непосредственно на изменениях, которые претерпевает котик.