Книги
Статистика и котики
Из предыдущей главы вы узнали, как определить, что делает наших котиков счастливыми. Для этих целей мы использовали корреляционный анализ. Однако коэффициенты корреляции позволяют установить лишь само наличие и выяснить направление этой связи. Определить, насколько сильно изменяется одна переменная под воздействием другой, он не в силах. В качестве иллюстрации приведем пример.

На графиках изображены две линейные положительные взаимосвязи. Коэффициент корреляции в обоих случаях равен +1. Однако очевидно, что каждый подранный диван делает котиков гораздо счастливее, чем очередное увеличение пайков. Эта разница математически описывается с помощью коэффициента b1. Он определяется как тангенс угла между линией котиков и горизонтальной оси x. Чем больше этот коэффициент, тем сильнее растет уровень счастья от каждой новой порции.
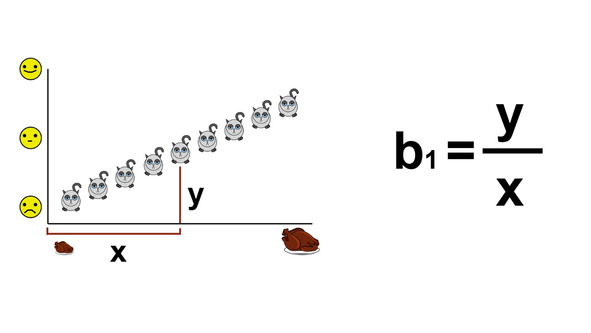
Можно выразиться и так: при увеличении порции мяса на одну единицу котиковое счастье будет возрастать на b1.
Вторая величина, которая может описывать нашу прямую, называется b0. Она показывает, насколько счастливы котики, если их совсем не кормить.

По итогу, линейную взаимосвязь между количеством еды и котиковым счастьем можно описать с помощью вот такого несложного уравнения.
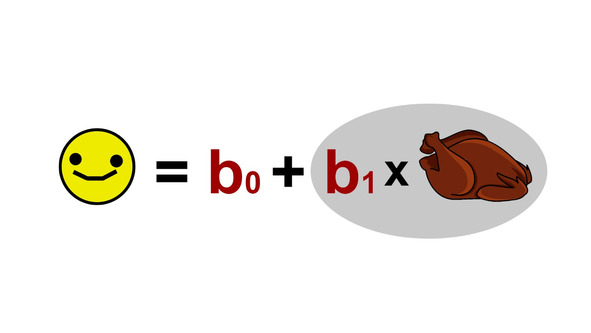
Однако, к сожалению, реальные взаимосвязи мало похожи на прямую линию. Чаще они напоминают собой огурец, а в запущенных случаях — авокадо. Но описывать такие вещи довольно сложно, поэтому статистиками был разработан специальный метод, который позволяет подобрать такую прямую, которая смогла бы заменить этот овощ с минимальными потерями данных. Этот метод называется

Рассмотрим, как это получается. Предположим, у нас есть прямая, полученная в результате регрессионного анализа, и недалеко от этой прямой обосновался наш старый знакомый — Барсик. На рисунке видно, что Барсик чуть менее счастлив, чем ему положено при своем рационе. Это различие называется
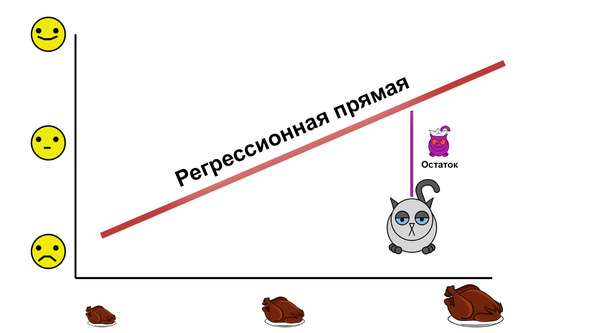
Теперь мысленно подвигаем Барсика относительно регрессионной прямой — при удалении от нее остаток будет увеличиваться, а при приближении — уменьшаться. И, наконец, если Барсик встанет на эту прямую, остаток будет равен нулю. А теперь вспомним, что у нашего Барсика есть компания, и если все наши котики находятся на прямой, то их совокупный остаток тоже будет равен нулю. В то же время при удалении от этой прямой совокупный остаток начнет увеличиваться.

Логика диктует, что, чтобы получить такой совокупный остаток, нам нужно просто сложить индивидуальные остатки котиков (бр-р-р… звучит жутко). Однако, поскольку эти остатки могут быть как положительными, так и отрицательными (некоторые котики ведь могут быть более счастливыми, правда?), на выходе мы можем получить полную белиберду (аналогичная ситуация была, когда мы считали стандартное отклонение). Поэтому, чтобы исключить влияние знаков, мы складываем квадраты остатков.
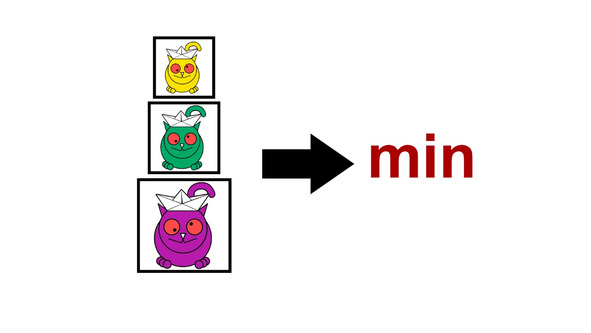
Чем больше получившаяся сумма, тем хуже прямая описывает наши данные. И суть регрессионного анализа заключается в том, чтобы подобрать такую прямую, при которой эта сумма была бы минимальной.
А теперь пару слов о том, почему регрессионный анализ считается одним из самых крутых статистических методов. Дело в том, что он способен работать с большим количеством переменных одновременно. И если вы умудритесь провести тотальный замер ваших котиков на предмет того, что может приносить им счастье, и прогоните эти данные через регрессионный анализ, вы можете получить настоящую формулу счастья.
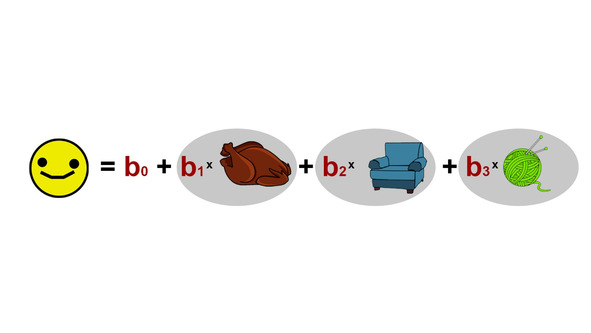
По этой формуле вы сможете выяснить, какие факторы наиболее сильно влияют на котиковое счастье, и предсказывать, насколько будет счастлив тот или иной котик по их значениям.
Однако здесь важно сделать предостережение — если вы вычислили такую формулу, это вовсе не означает, что то, что в ней справа — причины, а слева — следствие. В конце концов, может быть, еда делает котиков счастливыми, а может, и наоборот — у счастливых котиков лучше аппетит.
Помимо самой формулы вы также можете получить информацию о том, можно ли в нее что-нибудь добавить. В этом вам поможет коэффициент детерминации R2. Он изменяется в промежутках от 0 до 1, и чем ближе к единице, тем лучше ваша формула объясняет наблюдаемые данные. Низкий коэффициент детерминации говорит о том, что нужно поискать, какие еще переменные могут быть связаны с котиковым счастьем.
НЕМАЛОВАЖНО ЗНАТЬ!
Нелинейная регрессия
Вообще-то говоря, связь между переменными не всегда является линейной. Например, существует определенный момент, после которого котика начинает тошнить от дополнительных порций, хотя до этого момента каждая новая порция делала его более счастливым.

Такую взаимосвязь можно описать с помощью
Определить целесообразность использования этого или сходных с ним методов можно, предварительно построив точечные диаграммы. Помимо линейных и полиномиальных взаимосвязей могут быть еще и такие.
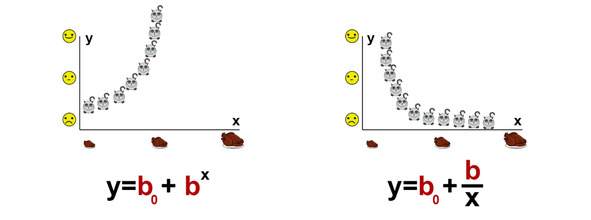
Увидев, что ваша взаимосвязь похожа на что-нибудь из этого, вы можете либо найти подходящий метод регрессионного анализа, либо преобразовать одну из переменных таким образом, чтобы можно было бы воспользоваться методами линейной регрессии.