Книги
Статистика и котики
Сложные эксперименты
Некоторое время назад мы рассмотрели, как правильно обрабатывать простые эксперименты с двумя группами и двумя замерами (до и после воздействия). Однако если групп и замеров больше, то наша задача существенно усложняется.
К примеру, мы разделили наших котиков на три группы: первой мы даем лекарство (экспериментальная), второй не даем лекарство (контрольная), а третьей даем пустышку, но говорим им, что дали лекарство (
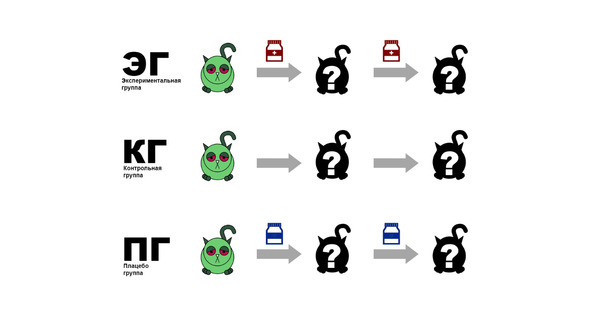
Для обработки такого исследования нам необходим двухфакторный дисперсионный анализ с повторными измерениями. Подобно обычному двухфакторному ДА такой анализ легче всего интерпретируется с помощью графиков.
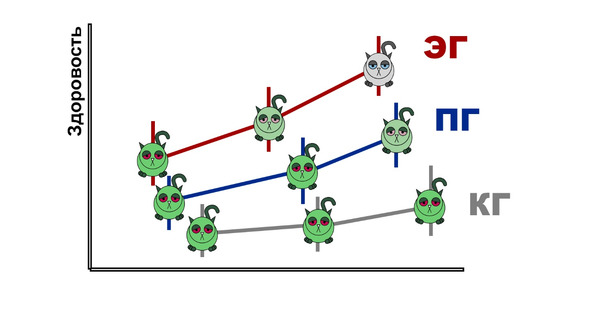
В частности из этого графика мы можем увидеть, что котики, принимавшие лекарство, выздоровели, плацебо-котикам стало чуть лучше, а контрольные котики так и продолжают болеть. Правда, возможно, на наши результаты могли повлиять небольшие различия между котиками в начале эксперимента.
К слову, все попарные различия между группами в разные моменты также необходимо проверять с помощью post hoc критериев. В частности — с помощью поправки Бонферрони.
Глава 9.
Как сделать котика счастливым
или основы корреляционного анализа
Безусловно, мы все хотим, чтобы наши котики были счастливы, и поэтому стараемся их постоянно радовать. Однако разных котиков радуют разные вещи: один любит вкусно поесть, другой — поиграть, а третий — поточить когти о любимый хозяйский диван.

Безусловно, существуют и некоторые универсальные вещи, которые радуют большинство котиков, что сильно упрощает нам жизнь. И в этой главе мы рассмотрим один из методов, который позволяет их выявить, —
Предположим, мы решили проверить, связаны ли между собой котиковое счастье и размер ежедневных котиковых порций. Если обильная еда делает котиков счастливыми, то эта взаимосвязь будет отражаться вот таким графиком.
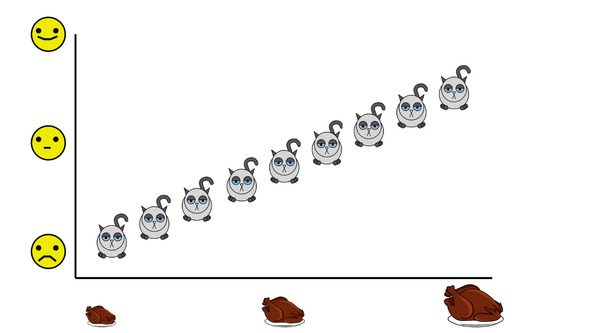
Это так называемая
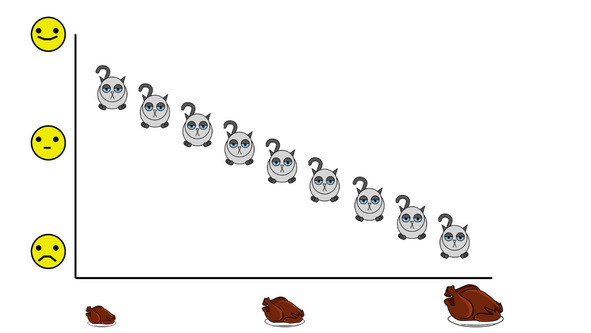
Такая связь называется

Однако в реальной жизни мы очень редко можем наблюдать подобные случаи: как правило, у нас возникает что-нибудь такое.
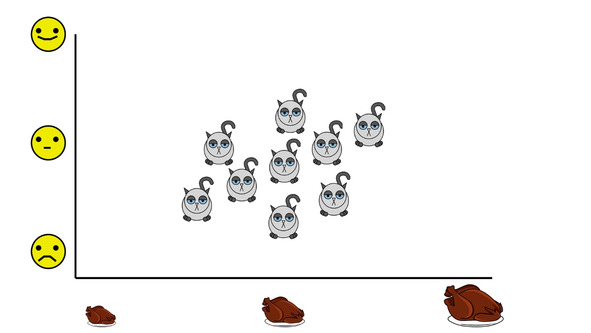
И поэтому мы нуждаемся в некоторой мере, которая позволила бы нам, во-первых, оценить, насколько сильно связаны между собой счастье и количество доступной еды, а во-вторых, является ли эта связь положительной или отрицательной.
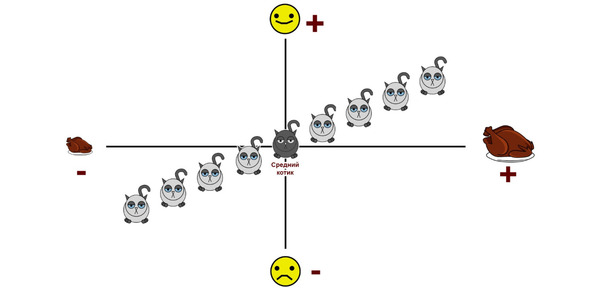
Для вычисления такой меры воспользуемся хитрым способом. Для начала представим, что у нас наблюдается линейная положительная связь. Теперь посчитаем средние арифметические по размеру порций и уровню счастья, а затем возьмем эти показатели в качестве нулевых точек отсчета для нашего графика. После этого мы можем увидеть, что часть котиков более счастлива и получает больше еды, чем в среднем, а остальные — менее счастливы и получают меньше еды, чем средний котик.
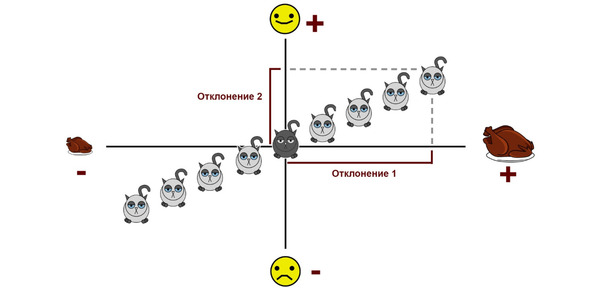
Отклонения от среднего по обеим величинам у первых, зажиточных котиков будут положительными числами, а у вторых — отрицательными. Однако если вы возьмете любого из них (назовем его Барсиком) и перемножите его отклонения между собой, то вы получите положительное число. В том числе и потому, что минус на минус дает плюс.
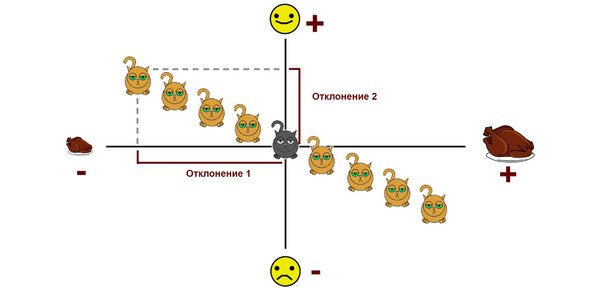
Теперь представим обратную ситуацию: чем больше порции, тем менее счастливыми становятся котики (типичного представителя этой группы мы назовем Мурзиком). В этом случае мы также наблюдаем разделение на две группы: несчастных обжор и счастливых голодающих. Но и у тех, и у других знак одного отклонения будет положительным, а знак другого — отрицательным. А как мы знаем, произведение положительного и отрицательного чисел дает отрицательное число.
Иными словами, знак, который получается при перемножении отклонений, может служить индикатором того, является ли наш котик Барсиком, который становится счастливее при увеличении порций, либо Мурзиком, которому еда отвратительна. Осталось только понять, кто из них делает больший вклад в наблюдаемые данные, что достигается простым суммированием полученных произведений. Если при результате стоит плюс, то победили Барсики и связь положительная. Если минус — то преобладают Мурзики и связь отрицательная. Если же ответ близок к нулю, объявляется боевая ничья и признается отсутствие связи.