Рациональность. Что это, почему нам ее не хватает и чем она важна, Стивен Пинкер

Книги

Рациональность. Что это, почему нам ее не хватает и чем она важна

22
18
20
22
24
26
28
30

Дженнифер: Я бы с тобой кофе пить не пошла.

Оливер: Да я бы тебя и не позвал.

Дженнифер: Потому-то ты и глупый.

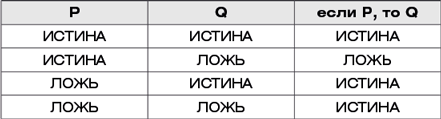
Давайте переформулируем слова Дженни так: «Если бы ты позвал меня выпить кофе, то я бы отказалась». Что мы можем сказать об истинности этого высказывания, учитывая все, что нам уже известно? Это импликация, то есть условное высказывание, построенное по формуле если (антецедент) — то (консеквент). Как выглядит его таблица истинности? Напомню, что, как мы знаем из обсуждения задачи выбора Уэйсона (глава 1), суждение «если Р, то Q» будет ложным, только если Р — ИСТИНА, а Q — ЛОЖЬ. (Высказывание «Если письмо отправляется экспресс-почтой, то на конверте должна быть марка за десять долларов» означает, что письмо без десятидолларовой марки экспресс-почтой не отправишь.) Вот эта таблица:

Если верить нашим студентам на слово, Оливер не позвал бы Дженни пить кофе. Другими словами, Р — ЛОЖЬ, а это значит, что условное высказывание Дженни истинно в любом случае (строки 3 и 4, третья колонка). Согласно таблице, неважно, как на самом деле она ответила бы на просьбу Оливера: если Оливер никогда не позовет ее в кафе, девушка говорит правду. Однако завершающая сцену насмешливая фраза Дженни позволяет предположить, что в один прекрасный момент Оливер все-таки пригласит ее выпить кофе (значение Р поменяется с ЛОЖЬ на ИСТИНА) и она согласится (Q — ложь). А это значит, что ее условное высказывание «если Р, то Q» было ложным, как нередко случается в игривых пикировках.

Логический сюрприз, на который мы здесь наткнулись, — условное высказывание всегда истинно, пока его антецедент ложен (если Оливер так и не позовет ее пить кофе, Дженни говорит правду) — наглядно демонстрирует, чем логическая импликация отличается от утверждения со словами «если» и «то» в обыденной речи. Мы чаще всего прибегаем к условному суждению, чтобы сделать обоснованный прогноз на базе поддающегося проверке причинного закона, например: «Если пить кофе, то не уснешь». Мы не готовы назвать истинным условное высказывание просто потому, что оно ни разу не проверялось, например: «Если пить брюквенный сок, то не уснешь», несмотря на то что оно будет логически истинным, если вы никогда не пили брюквенный сок. Нам нужны основания, чтобы поверить, что в гипотетической ситуации, где Р — истина (вы пьете брюквенный сок), не Q (вы уснете) не случится. Зная, что антецедент условного высказывания — ложь или заведомая ложь, мы скорее сочтем высказывание неуместным, неактуальным, надуманным или даже бессмысленным, но никак не истинным. Однако в строго логическом смысле, описанном таблицами истинности, где «если Р, то Q» — всего лишь синоним «не [Р и не Q]», истинными будут и такие странные утверждения, как «Если у поросят есть крылья, то 2 + 2=5» и «Если 2 + 2=3, то 2 + 2=5». По этой причине специалисты в области логики используют для условного высказывания в смысле таблиц истинности особый технический термин «материальная импликация».

Чтобы показать значимость этого различия, приведу пример из жизни. Предположим, нам нужно оценить точность предсказаний, сделанных аналитиками. Как оценить условный прогноз 2008 г.: «Если Сара Пэйлин станет президентом, она запретит аборты»? Стоит ли нам похвалить аналитиков, поскольку, рассуждая логически, это утверждение истинно? Или же истинность в смысле законов логики здесь не в счет? В ходе реального состязания прогнозистов, откуда и взят этот пример, экспертам пришлось задуматься, что делать с такими прогнозами, и в итоге они постановили не считать их истинными — подобные импликации решено было понимать в житейском смысле, а не в строго логическом[116].

Разница между «если» в обыденной речи и логическим если — лишь один пример того, что мнемонические символы, применяемые в качестве операторов формальной логики, не тождественны аналогичным словам живого языка, где у них, как и у всех прочих слов, есть масса значений, а конкретный смысл раскрывается в контексте[117]. Союз «и» в предложении «Он уселся и поведал мне свою историю» сообщает, что человек, о котором идет речь, сделал сначала одно, а затем другое, хотя логически все могло быть ровно наоборот (как в шутке из другой эпохи: «Они поженились и завели ребенка — только в обратном порядке»). Когда грабитель говорит: «Кошелек или жизнь», технически вы можете сохранить и то и другое, поскольку выражение «Р или Q» будет истинным и тогда, когда истинно и Р, и Q. Но я бы не советовал объяснять эту мысль бандиту; в данном контексте все без исключения понимают «или» как логический оператор «исключающее или»: «Р или Q и не [Р и Q]». Именно поэтому, если меню бизнес-ланча предлагает на выбор «суп или салат», мы не станем доказывать официанту, что с точки зрения логики нам полагается и то и другое. Наконец, заявления вроде «Мальчишки остаются мальчишками», «Сделка есть сделка» и «Иногда сигара — это просто сигара» — строго говоря, пустые тавтологии, неизменно истинные из-за своей формы и в то же время лишенные всякого содержания. Но нам удается извлечь из них смысл; из последнего примера (приписываемого Зигмунду Фрейду) мы узнаем, что сигара — не всегда фаллический символ.

* * *

Даже если слова употреблялись бы только в их строго логическом значении, логика оставалась бы малозначительным упражнением, умей она лишь устанавливать истинность утверждений, содержащих логические связки. Своим потенциалом она обязана правилам, позволяющим делать истинные выводы, — коротким алгоритмам, описывающим путь от истинных посылок к истинным заключениям. Самое известное из них называется подтверждением антецедента или утверждающим модусом (посылки размещены над линией, заключения — под ней):

«Если некто — женщина, то она смертная. Ксантиппа — женщина. Следовательно, Ксантиппа — смертная». Еще одно надежное правило вывода называют отрицанием консеквента, законом контрапозиции или отрицающим модусом:

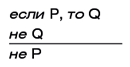
«Если некто — женщина, то она смертная. Горгона Сфено — бессмертная. Следовательно, горгона Сфено — не женщина».

Это самые известные, но, конечно, не единственные верные правила вывода. С момента, когда Аристотель впервые формализовал логику, и до конца XIX в., когда ее законы начали оформлять математически, логика прежде всего описывала способы, какими можно и нельзя вывести заключение из совокупности посылок. Существует, к примеру, верное (и по большей части бесполезное) дизъюнктивное сложение:

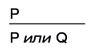
«Париж находится во Франции. Следовательно, Париж находится во Франции или единороги существуют». Дизъюнктивный силлогизм, он же процесс элиминации, оказывается более полезным:

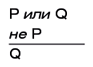
«Жертва была убита свинцовой трубой или канделябром. Жертва была убита не свинцовой трубой. Следовательно, жертва была убита канделябром». Есть такой анекдот: однажды логик Сидни Моргенбессер и его девушка проходили сеанс психотерапии для пар, во время которой без конца препирались и жаловались друг на друга. В конце концов доведенный до белого каления психотерапевт сказал: «Слушайте, кому-то нужно измениться». На что Моргенбессер ответил: «Ну, я-то меняться не собираюсь, и она тоже. Так что придется меняться вам».

Еще интереснее «принцип взрыва», также известный под названием «из противоречия можно вывести все, что угодно»:

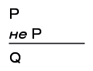
Предположим, вы считаете, что Хекстейбл находится в Англии (Р). Одновременно вы уверены в истинности не Р: Хекстейбл находится не в Англии. По правилу логического сложения вы можете перейти от Р к [Р или Q]: «Хекстейбл находится в Англии, или единороги существуют». Затем, по правилу дизъюнктивного силлогизма, ничто не мешает перейти от [Р или Q и не Р] к Q: «Хекстейбл находится не в Англии. Следовательно, единороги существуют». Мои поздравления! Вы только что логически доказали, что единороги существуют. Люди часто неверно цитируют Ральфа Уолдо Эмерсона, который якобы сказал: «Постоянство — это химера ограниченного ума». На самом деле он писал о глупом постоянстве, от которого «великие умы» должны избавляться, но в любом случае выпад сомнительный[118]. Если ваша система верований внутренне противоречива, вы можете уверовать во что угодно. (Моргенбессер сказал однажды о философе, которого ценил невысоко: «Это человек, который одновременно провозгласил Р и не Р, а затем вывел из этого все возможные следствия»[119].)

Тот факт, что верные правила вывода порой приводят к абсурдным заключениям, сообщает нам о логических рассуждениях нечто очень важное. Чтобы рассуждение было валидным, достаточно корректно применить к посылкам правила вывода. Все, на что такое рассуждение способно, так это сообщить: если посылки истинны, то и заключения должны быть истинными. Оно ничего не говорит о том, истинны ли посылки, и, следовательно, не гарантирует истинности заключения. Ему можно противопоставить обоснованное рассуждение, которое верно применяет правила вывода к истинным посылкам и, соответственно, приходит к истинному заключению. Вот валидное рассуждение: «Если Хиллари Клинтон выиграет выборы 2016 г., то в 2017 г. Тим Кейн станет вице-президентом. Хиллари Клинтон выиграла выборы 2016 г. Следовательно, в 2017 г. Тим Кейн занял должность вице-президента». Однако это рассуждение не обоснованно, поскольку Клинтон не победила на выборах в 2016 г. А вот рассуждение: «Если Дональд Трамп победит на выборах 2016 г., то в 2017 г. Майк Пенс станет вице-президентом. Дональд Трамп выиграл выборы 2016 г. Следовательно, в 2017 г. Майк Пенс стал вице-президентом» — и валидно, и обоснованно.

Подавать валидное рассуждение как обоснованное — распространенная ошибка. Политики обещают: «Если мы положим конец растратам и коррупции среди чиновничества, то сможем понизить налоги, повысить доходы и сбалансировать бюджет. Я положу конец растратам и коррупции. Итак, голосуйте за меня, и все наладится». К счастью, люди, как правило, замечают, что таким рассуждениям не хватает обоснованности; у нас есть чем возразить софисту, который выводит правдоподобные умозаключения из сомнительных посылок: «Это еще бабушка надвое сказала», «Если бы да кабы, во рту росли бы грибы», «Возьмем сферическую корову в вакууме» (это выражение, распространенное в научной среде, обязано своим происхождением анекдоту о физике, нанятом фермером для разработки плана повышения удоев). Мое любимое подобное возражение звучит на идише так: As di bubbe volt gehat beytsim volt zi gevain mayn zaidah («Если бы у моей бабушки были яйца, она была бы моим дедушкой»).

Безусловно, существует масса рассуждений, которые даже валидными не назовешь. Специалисты по классической логике также составили перечень ненадежных рассуждений, или формальных ошибок, то есть таких последовательностей высказываний, где заключения на первый взгляд выводятся из посылок, но на самом деле это не так. Самая известная такая ошибка называется подтверждением консеквента: «Если Р, то Q. Q. Следовательно, Р». Если идет дождь, то улицы мокрые. Улицы мокрые. Следовательно, идет дождь. Это невалидное рассуждение: может, по улице проехала поливальная машина. Еще одна похожая ошибка — отрицание антецедента: «Если Р, то Q. не Р. Следовательно, не Q». Дождь не идет, следовательно, улицы не мокрые. Это рассуждение тоже невалидно, по той же самой причине. Проще говоря, утверждение «Если Р, то Q» не подразумевает ни обратного — «Если Q, то Р», ни противоположного — «Если не Р, то не Q».

Однако люди довольно часто прибегают в своих рассуждениях к подтверждению консеквента, путая «Р предполагает Q» с «Q предполагает Р». Вот почему в задаче выбора Уэйсона столь многие, кого просили проверить истинность высказывания «Если D, то 3», переворачивали карточку с тройкой. Вот почему консервативные политики внушают избирателям идею, что высказывание «Если некто социалист, он, вероятно, член Демократической партии» подразумевает и обратное: «Если некто член Демократической партии, он, вероятно, социалист». Вот почему безумцы заявляют, что над всеми великими умами в свое время насмехались, забывая, что «Если ты гений, то над тобой смеются» не предполагает, что «Если над тобой смеются, то ты гений». Эту мысль стоит держать в уме и лодырям, утешающим себя мыслью, что самые успешные хай-тек-компании были основаны студентами, бросившими колледж.

Назад Читать дальше