Книги
Жизнь и идеи Бруно Понтекорво

Красивый эксперимент, идея которого до сих пор используется по всех опытах с реакторными антинейтрино, заключался в детектировании гамма-квантов от аннигиляции позитрона в совпадении с сигналом от поглощения нейтрона. То есть сначала приходил гамма-квант с энергией 0,5 МэВ, а затем, приблизительно через 10 мкс (время, необходимое для поглощения теплового нейтрона) приходили гамма-кванты от захвата нейтрона.
Обратите внимание: сохранение лептонного числа требует, чтобы при взаимодействии антинейтрино (L = –1) в конечном состоянии реакции (19) должен появиться позитрон (L = –1), а не электрон (L = +1). Но в те времена, чем отличается нейтрино от антинейтрино, никто ясно не представлял, и Дэвис хотел попробовать с помощью реакторных антинейтрино сделать опыт Понтекорво по образованию аргона-37
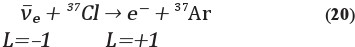
Но Бруно предлагал эту реакцию для взаимодействия нейтрино:
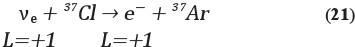
Тут все законно – лептонное число сохраняется. Поэтому, когда появились слухи о том, что Дэвис видит какие-то события от реакции (20) то, казалось, это говорит о несохранении лептонного числа.
Но Бруно предложил другое оригинальное объяснение: что если реакторные антинейтрино по пути к детектору превращаются в нейтрино? То есть происходит цепочка процессов:
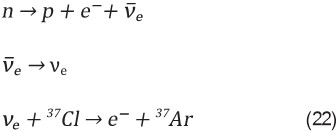
Но какой процесс мог бы обеспечить переход антинейтрино в нейтрино νe?
Бруно предложил, что антинейтрино переходит в нейтрино νe за счет феномена осцилляций, подобных тем, что наблюдаются в системе нейтральных К-мезонов.
В первом же абзаце своей исторической работы 1957 г. «Мезоний и антимезоний» [105] он пишет:
«Гелл-Манн и Пайс впервые указали на интересное следствие, вытекающее из того факта, что K0 и K—0 не являются тождественными частицами. Вероятность превращения K0 → K—0, вызываемого слабыми взаимодействиями, приводит к тому, что нейтральные К-мезоны необходимо рассматривать как смесь частиц K10 и K20, имеющих разную комбинированную четность. В настоящей заметке обсуждается вопрос, существуют ли иные “смешанные” нейтральные частицы (не обязательно “элементарные”), кроме K0 мезонов, которые отличаются от соответствующих античастиц, причем переходы частица → античастица не являются строго запрещенными».
Что такое осцилляции нейтральных К-мезонов? Как мы уже говорили, мезоны K0 и K—0 отличаются флейворным квантовым числом странностью S. Странность К0-мезона S = +1. Странность K—0-мезона S = –1. В сильных взаимодействиях странность сохраняется. Если бы мы жили в Сильном мире, где существуют только сильные взаимодействия, то переходы

были бы строго запрещены. Но в реальном мире есть еще и слабое взаимодействие, в котором странность не сохраняется. Поэтому в Сильно-Слабом мире переходы K0 в K—0 могут проходить через промежуточные состояния с нулевой странностью, типа:
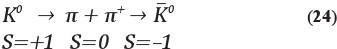
На первый взгляд, это означает, что если бы мы создали пучок чистых K0, то со временем они бы все просто перетекли в K—0. Однако K—0 тоже могут переходить в K0. Поэтому ситуация становится намного интереснее. Условно она показана на Рис. 34-1.
Если приготовить в начальном состоянии пучок чистых К0-мезонов и позволить ему свободно распространяться, то со временем число К0-мезонов сначала действительно будет уменьшаться, причем в пучке К0 начнут возникать K—0-мезоны, что соответствует нашим интуитивным ожиданиям. Но если мы продолжим наблюдения, то увидим, что число К0-мезонов перестанет падать и даже начнет увеличиваться, а число K—0-мезонов, соответственно, уменьшаться (см. Рис. 34-1). Такие вариации числа К0-мезонов будут продолжаться и дальше с уменьшающейся амплитудой. Этот эффект называется осцилляциями в системе К0-K—0-мезонов.
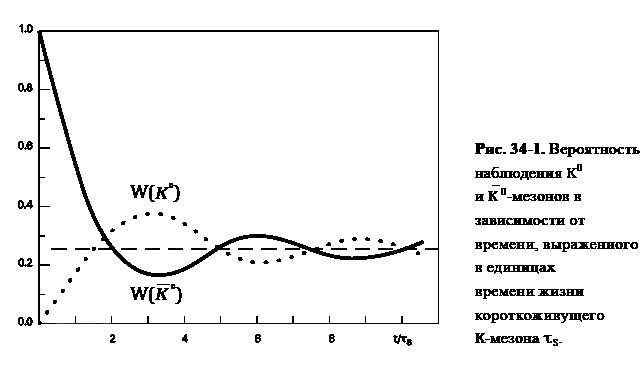
Рис. 34-1. Вероятность наблюдения K0 и K—0-мезонов в зависимости от времени, выраженного в единицах времени жизни короткоживущего K-мезона τS.
В нашем повседневном мире, казалось бы, нет ничего подобного осцилляциям каонов. Конечно, русскую народную песню «Летят утки, летят утки и два гуся» можно рассматривать как рассказ о том, что в момент t0 летели утки, а в момент t1 в стае уток появилось два гуся. Но поскольку в песне не прослеживается, что в дальнейшем, по мере движения, число уток опять восстанавливается, мы не можем считать это полноценным описанием осцилляций в системе утки-гуси.
Однако механический аналог явления осцилляций каонов существует. Это два маятника, связанные слабой пружинкой. Такую игрушку подарили Бруно на 70-летие Л. Микаэлян и А. Боровой из Курчатовского института.
Если отклонить один из маятников, на Рис. 34-2 он справа, то скоро его колебания начнут затухать, а другой, левый, маятник начнет раскачиваться со все более возрастающей амплитудой. Затем процесс повторится: левый маятник замедлит свои колебания, а колебания правого маятника начнут возрастать. Если закрыть экраном один из маятников, то можно показывать изумленному зрителю фантастический маятник с переменным периодом колебаний[34].
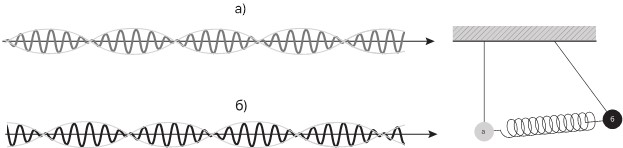
Рис. 34-2. Осцилляции в системе связанных маятников.
Осцилляции каонов возникают за счет красивого квантового эффекта интерференции амплитуд процессов с частицами разной массы. В Сильном мире массы K0 и K—0 строго одинаковы. Но включение слабого взаимодействия приводит к расщеплению единого уровня K0 и K—0 на два состояния – K10 и K20 с разными массами[35]. То есть, вброшенные в мир Слабых взаимодействий, K0 и K—0 начинают ощущать, что являются смешанными состояниями из симметричной [36] и антисимметричной комбинаций K10 и K20:
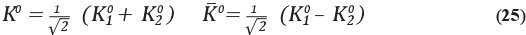
Разность масс K10 и K20 фантастически мала (и это крайне существенно для возникновения осцилляций):