Книги
Тайны чисел: Математическая одиссея
Полагается, что если какой-либо пузырь не подчиняется правилам Плато, то он нестабилен, следовательно, должна произойти перестройка конфигурации в стабильную, подчиняющуюся этим правилам. Лишь в 1976 г. Джин Тейлор окончательно доказала, что форма пузырьков в пене должна подчиняться правилам, установленным Плато. Ее работа говорит нам о том, как пузыри объединяются, но какова же фактическая форма пузырей в пене? Поскольку пузыри ленивы, появляется возможность ответить на этот вопрос, если найти формы пузырей в пене, каждая из которых охватывает заданный объем воздуха и при этом минимизирует площадь мыльной пленки.
Медоносные пчелы уже решили эту задачу в двух измерениях. Причина, по которой они сооружают соты, используя шестиугольники, состоит в том, что при этом требуется наименьшее количество воска при фиксированном количестве меда в каждой ячейке. Но опять-таки лишь благодаря недавнему прорыву удалось доказать теорему о медовых сотах: никакая другая двумерная структура не превзойдет шестиугольные соты по эффективности.
Тем не менее, когда мы переходим к трехмерным структурам, положение вещей становится менее очевидным. В 1887 г. знаменитый британский физик лорд Кельвин предположил, что один из Архимедовых футбольных мячей играет ключевую роль в минимизации площади поверхности в пене. В то время как шестиугольник является строительным кирпичиком при сооружении эффективных пчелиных сот, усеченный октаэдр определяет построение пены. Усеченный октаэдр получается срезанием шести углов обычного октаэдра:

Правила, которые установил Плато для пересечения пузырей, показывают, что грани и ребра должны быть не плоскими, а изогнутыми. Например, стороны квадрата образуют угол 90°, но по второму правилу Плато это недопустимо. Вместо этого края квадрата должны немного выгибаться наружу, как в случае кубического проволочного каркаса, тогда между ними образуется необходимый угол 109,47°.

Многие считали, что структура Кельвина является ответом на вопрос, как получить пену с минимальной поверхностной энергией, но никто не мог доказать этого. Но в 1993 г. Денис Уэйр и Роберт Фелан из Дублинского университета обнаружили две формы, которые при совместной упаковке превосходят структуру Кельвина на 0,3 % (пусть это послужит предупреждением тем, кто полагает, что доказательство в математике – напрасная трата времени).
Использованные ими формы не были в списке Архимеда. Гранями первой из них являются неправильные пятиугольники, они объединены в искаженный додекаэдр (пентагондодекаэдр). Вторая форма называется тетракаидекаэдр, ее грани – два удлиненных шестиугольника и 12 неправильных пятиугольников двух видов. Уэйр и Фелан выяснили, что они могут упаковать эти формы вместе, так что получится более эффективная пена, чем предложенная Кельвином. Опять-таки, чтобы удовлетворить правилам Плато, нужно немного искривить ребра и грани. Оказывается, довольно трудно проникнуть внутрь настоящей пены, чтобы посмотреть, что происходит на самом деле. Двое ученых проводили численные эксперименты, использовали компьютеры для моделирования пены и обнаружили новую структуру.
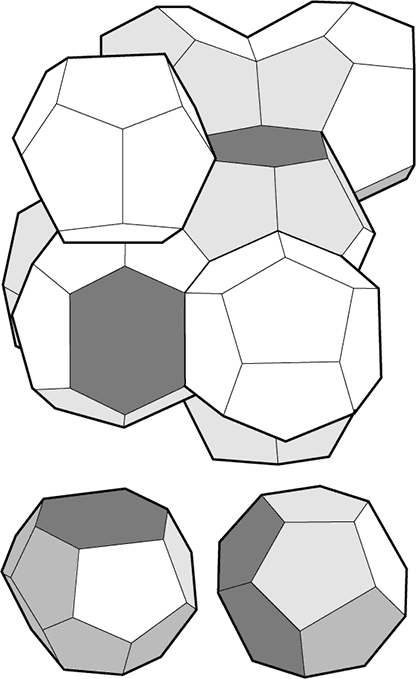
Это – лучшее, на что способны пузыри? Мы не знаем. Мы считаем, что данная структура наиболее эффективна. Но ведь и Кельвин полагал, что нашел ответ.
Дизайнеры Arup в своем поиске интересных природных форм, напоминающих о состязаниях, проходящих в олимпийском плавательном комплексе, изучали туман, айсберги и волны. Они случайно натолкнулись на пену Уэйра – Фелана и поняли, что у нее был потенциал к созданию совершенно новых архитектурных форм. Чтобы избежать чрезмерной регулярности, решили разрезать пену под углом. Внешние стены «Водяного куба», как неформально называется плавательный центр, представляют ту структуру пузырей, которую вы увидите, если вставите лист стекла в пену под углом.
Хотя структура, созданная Arup, кажется вполне случайной, она начинает повторяться на протяжении здания. Тем не менее она вызывает именно то органичное ощущение, к которому стремились дизайнеры. Однако если вы получше приглядитесь, то заметите пузырь, который противоречит правилам Плато, ведь в его очертаниях заметны прямые углы вместо предписанных Плато 120° и 109,47°. Так стабилен ли «Водяной куб»? Будь он сделан из пузырей, ответом было бы «нет». Данный прямоугольный пузырь изменил бы свою форму, чтобы прийти в соответствие тем математическим правилам, которым должны подчиняться все пузыри. И все-таки у китайских властей нет повода для беспокойства. Насколько можно ожидать, «Водяной куб» будет стоять благодаря математике, которая была задействована при создании этого прекрасного сооружения.

Но не только Arup и китайские власти интересуются формой, которую приобретают пузыри, когда их прижимают друг к другу. Понимание строения пены помогает нам разобраться во многих других природных структурах, например в структуре органических клеток в шоколаде, взбитых сливках или в шапке над пинтой пива. Пена используется при тушении пожаров, в защите водных ресурсов от радиоактивных утечек и при переработке минералов. Интересуетесь ли вы борьбой с пожарами или тем, как добиться, чтобы пенная шапка над вашим «Гиннессом» не оседала слишком быстро, ключ к ответу определяется пониманием математической структуры пены.
Почему у снежинки шесть лучей?
Одним из первых, кто попытался дать математический ответ на этот вопрос, был астроном и математик XVII в. Иоганн Кеплер. Его понимание того, почему у снежинки шесть лучей, возникло после изучения плода граната. Зернышки граната начинают свой рост с маленьких шариков. Как знает любой продавец фруктов, наиболее эффективный способ заполнить пространство шарами состоит в расположении их слоями шестиугольников. Слои хорошо подгоняются друг к другу, когда каждый шар из последующего слоя находится между тремя шарами слоя под ним. Совместно эти четыре шара расположены так, что являются вершинами тетраэдра.
Кеплер предположил, что это самый эффективный способ заполнить пространство – другими словами, при таком размещении у промежутков между шарами будет минимальный объем. Но как можно быть уверенным, что не существует какого-то более сложного расположения шаров, способного улучшить данную упаковку шестиугольников? Гипотеза Кеплера, как стало называться его невинное утверждение, овладевала умами поколений математиков. Ее доказательство появилось в конце XX в., когда математики объединили свои силы с мощью компьютеров.
Но вернемся к плоду граната. По мере его роста зернышки начинают сдавливать друг друга, их поверхность превращается из сфер в формы, полностью заполняющие пространство. Каждое зернышко внутри плода находится в контакте с 12 другими, поэтому когда они сдавливают друг друга, получается форма с 12 гранями. Вы могли бы подумать, что она будет соответствовать додекаэдру с его 12 пятиугольными гранями, но додекаэдры нельзя сложить вместе, чтобы они заполнили все имеющееся пространство. Единственное Платоново тело, способное идеально состыковаться и заполнить пространство, – это куб. Вместо этого 12 граней зернышка граната приобретают форму ромба. Результирующий многогранник, называемый ромбододекаэдром, часто встречается в природе (рис. 2.19).

Так, у кристалла граната 12 граней в форме ромба. Английское слово