Книги
Тайны чисел: Математическая одиссея
Подкиньте две игральные кости. Число рыб, исходно имеющихся в аквариуме, равно сумме выпавших очков минус один (поэтому данное число лежит в диапазоне от 1 до 11). Назовем это число
Не все рыбы доживают до следующего года. Если в конце предыдущего года было

Комбинация с первым слагаемым в круглых скобках соответствует приведенному приросту количества рыб из-за рождения, а комбинация со вторым слагаемым – убыли рыб из-за смертности. Нужно округлить число, определяемое данной формулой, чтобы в аквариуме было целое число рыб (4,5 округляется до 5).
Пусть аквариум содержится на протяжении 10 лет. Счет первого игрока равен сумме количества рыб в конце нечетных лет, а счет второго игрока равен сумме количества рыб в конце четных лет.
То есть, если в конце года с номером
счет игрока 1:
счет игрока 2:
Делая отметки на боках вырезанных фигурок, вы можете вести учет численности рыб от года к году. Если в какой-то момент все рыбы умирают, игрок 1, выбравший множитель
Вот пример одной из игр. На игральных костях выпало 4. Поэтому сначала в аквариуме было 3 рыбы,

Количество рыб в конце второго года
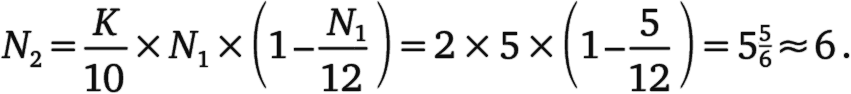
А в конце третьего года их
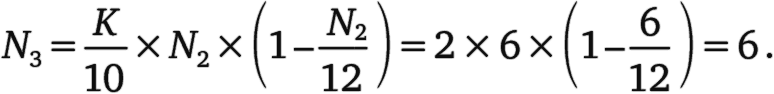
Количество рыб теперь стабилизировалось, потому что 6 будет повторяться при подстановке в формулу. Итак,
счет игрока 1: 5 + 6 + 6 + 6 + 6 = 29 рыб,
счет игрока 2: 6 + 6 + 6 + 6 + 6 = 30 рыб.
Игрок 2 побеждает. Посмотрите, что произойдет при изменении множителя
Если вы хотите воспользоваться онлайн-моделированием этой игры, пройдите по ссылке http://bit.ly/Tanksim.
В данной версии моделирования количество рыб в аквариуме также округляется до целого числа, но дробная часть числа подставляется в формулу для расчета количества рыб в следующем году. Например, если вы положите