Книги
Тайны чисел: Математическая одиссея
Даже если вы знаете математику, игры вроде «Монополии» или телевикторины «Тайн 4исел» все же опираются на случай. Но теперь я предложу вам простую игру для двух участников, которая иллюстрирует то, как математика может гарантировать вам победу. Возьмите 13 шоколадных батончиков и стручок жгучего перца и сложите их в кучку на столе. Каждый игрок по очереди берет один, два или три предмета из кучки. Цель игры состоит в том, чтобы заставить вашего соперника взять стручок перца.
Существует стратегия, приводящая к победе, если вы ходите первым. Она состоит в том, что, сколько бы батончиков ни взял соперник, вы берете из горки столько батончиков, чтобы в данном раунде вы вместе взяли четыре штуки. Например, если ваш оппонент берет три батончика, вы берете один. Если же он берет два, вы также берете два.
Прием состоит в том, что можно расположить батончики шоколада в ряды по четыре штуки (делайте это в голове, иначе вы раскроете свои карты). Вначале имеется 13 батончиков, то есть получается три ряда по четыре плюс один батончик (а также, разумеется, перец). Так что ваш первый ход должен состоять в том, чтобы взять этот одиночный батончик. После этого действуйте по рецепту, приведенному выше: в ответ на ход вашего соперника возьмите столько батончиков, чтобы вместе вы брали четыре. После трех раундов на столе останется только стручок перца, и вашему сопернику придется взять его.

Стратегия опирается на то, что вы ходите первым. Если первым ходит ваш оппонент, то единственной его ошибки будет достаточно, чтобы вы вернули себе выигрышную позицию. Например, если он возьмет больше одного батончика при первом ходе, он станет расходовать батончики из первого ряда из четырех штук. Тогда вы, как и ранее, возьмите остаток этого ряда.
Вы можете модифицировать игру, начав ее с другого количества батончиков или изменив максимальное число батончиков, которое разрешается брать за один ход. Та же математика, состоящая в разделении батончиков на группы, позволит вам придумать выигрышную стратегию.
Существует другой вариант этой игры, называемый «Ним». Для нахождения гарантированной выигрышной стратегии в «Ним» необходим более изощренный математический анализ. На сей раз на столе находятся четыре кучки. В первой кучке – пять шоколадных батончиков, во второй – четыре, в третьей – три, наконец, в четвертой находится только стручок перца. Теперь вам разрешается брать сколько угодно батончиков, но только из одной кучки. Например, вы могли бы взять все пять шоколадных батончиков из первой кучки либо только один из третьей. Вы проиграете, если вашей единственной возможностью будет взять стручок перца.

Чтобы выиграть эту игру, нужно уметь переводить числа из десятичной в двоичную систему счисления. Мы считаем десятками, потому что у нас десять пальцев. После того как вы дошли до 9, вы начинаете новый разряд в записи чисел и пишете 10, чтобы указать, что в этом числе один десяток и ноль единиц. Но компьютеры любят считать двойками, что мы называем двоичной, или бинарной, системой. Каждый разряд в записи числа в двоичном виде соответствует степени 2, а не степени 10. Например, двоичное число 101 подразумевает 1 набор 22, 0 наборов 21 и 1 единицу (20). Итак, 101 – это двоичный вид числа 4 + 1 = 5. В таблице приведено несколько первых чисел, записанные в двоичном виде.
Чтобы выиграть в игру «Ним», нужно перевести число батончиков в каждой кучке в двоичный вид. Тогда получится, что в первой кучке 101 батончик, во второй 100, а в третьей 11. Записывая последнее число как 011 и располагая эти числа в трех строках поверх друг друга, мы приходим к
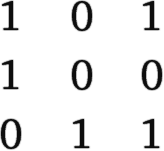
Заметьте, что в первом столбце содержится четное число единиц, во втором нечетное и в третьем четное. Выигрышная стратегия заключается в том, чтобы при каждом ходе убирать столько батончиков из одной из кучек, чтобы в каждом столбце получалось четное число единиц. Итак, в данном случае возьмите два батончика из третьей кучки, чтобы их число уменьшилось до 001.
Почему это поможет вам выиграть? Что же, каждый раз ваш соперник будет вынужден оставлять как минимум один столбец с нечетным числом 1. Вы последующим ходом возьмете столько батончиков, чтобы снова сделать число 1 во всех столбцах четным. Поскольку число батончиков постоянно уменьшается, в какой-то момент их не останется, так что в трех кучках будет 000, 000 и 000 батончиков. Кто сделает приводящий к этому ход? Ваш соперник всегда оставляет нечетное число 1 хотя бы в одной из кучек, поэтому этот ход сделаете вы. И оппоненту не останется ничего иного, как взять стручок перца.
Эта стратегия сработает независимо от числа батончиков в кучках. Вы даже можете увеличить количество кучек.
Почему магические квадраты играют ключевую роль в облегчении деторождения, предотвращении наводнений и победе в играх?
Умение взглянуть на проблему с разных сторон оказывается очень полезным, когда дело доходит до математики. Может оказаться так, что решение тяжелой головоломки неожиданно станет очевидным, если вы посмотрите на нее под другим углом. Искусство состоит в том, чтобы найти, как правильно рассматривать задачу. Иллюстрацией этому служит игра, обсуждаемая ниже. На первый взгляд довольно трудно следить за ее ходом, но если рассмотреть эту игру иначе, все становится довольно просто. Вы можете загрузить файл с веб-сайта «Тайн 4исел» и вырезать реквизит, необходимый для игры.
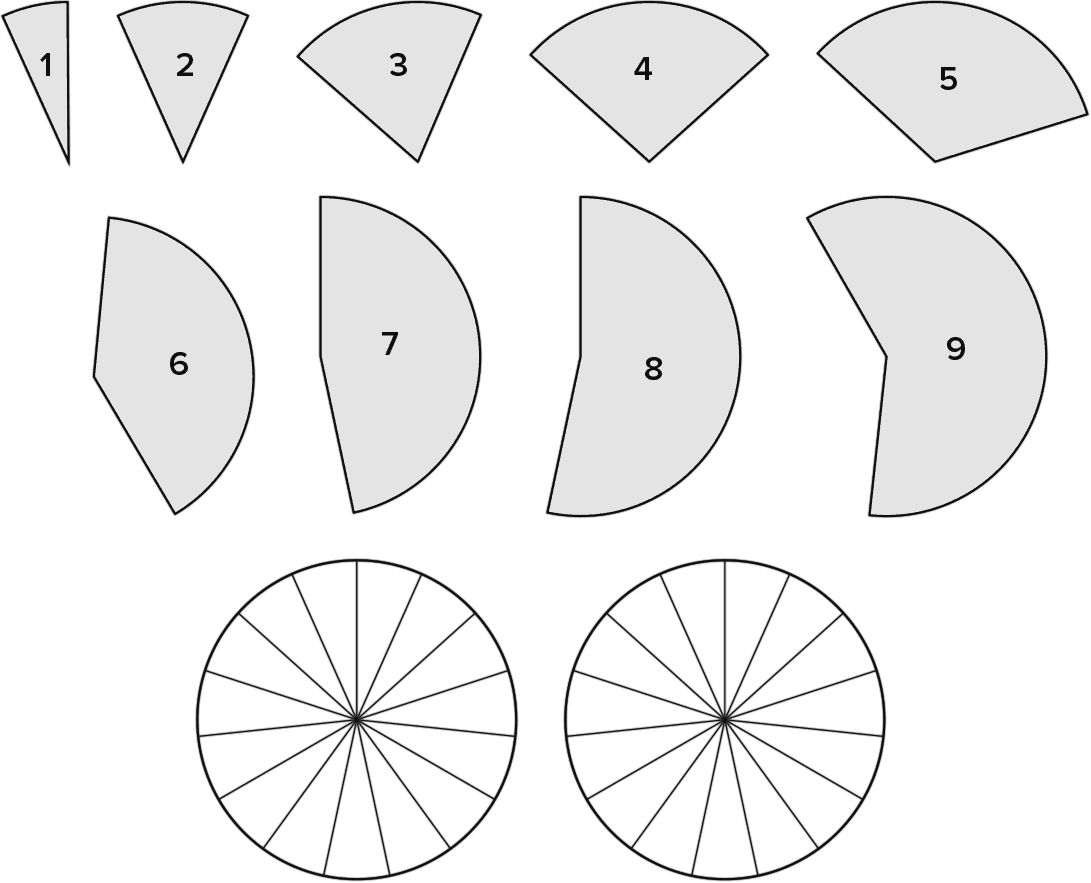
У каждого из участников есть пустое блюдо для торта, на которое помещается 15 кусков. Цель игры состоит в том, чтобы первым заполнить свое блюдо ровно тремя секторами из имеющихся девяти секторов разных размеров. Наименьший сектор содержит лишь один кусок, а наибольший – девять кусков. Соперники по очереди выбирают один из секторов.
Цель состоит в том, чтобы получить три числа от 1 до 9, которые в сумме дают 15, одновременно с этим нужно следить за тем, что делает ваш соперник, и расстроить его планы. Так, если ваш оппонент взял сектора с 3 и 8 кусками, необходимо не дать ему набрать 15, взяв сектор с 4 кусками. Если сектор, который вы присмотрели, уже был взят, требуется отыскать другой способ прийти к 15, используя взятые куски и остающиеся. Но заполнять блюдо нужно ровно тремя секторами – использование секторов с 9 и 6 кусками не будет считаться победой, как и заполнение блюда четырьмя секторами с 1, 2, 4 и 8 кусками.
Вскоре после начала игры становится довольно трудно уследить за различными способами, которыми вы и ваш соперник можете заполнить блюда. Но игра становится значительно проще, когда вы поймете, что, по существу, играете в замаскированную классическую игру крестики-нолики. Вместо обычной сетки 3 × 3, на которую вы помещаете 0 и Х, стараясь расположить три в линию до вашего соперника, это состязание разыгрывается на магическом квадрате: