Книги
Постигая Agile
Теперь у них есть все данные, которые нужны для построения CFD.
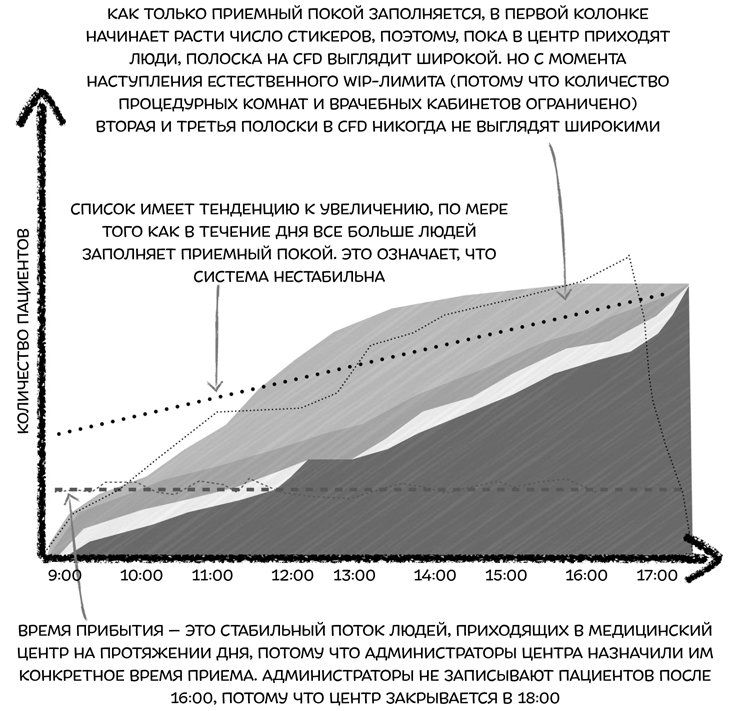
Эта система нестабильна. Скорость прибытия пациентов стабильна, потому что администраторы сами назначают время приема пациентов, а те, в свою очередь, приходят с постоянной скоростью. Администраторы не хотят задерживаться на работе. Поэтому прекращают запись после 16:00. Люди попадают к врачу позже назначенного времени, но тенденция скорости прибытия плоская, поэтому она должна быть довольно постоянной на протяжении всего дня.
Тенденция очереди, однако, не является плоской. Она стремится вверх, потому что очередь растет. В этом есть смысл – количество пациентов в приемном покое также увеличивается на протяжении дня. Каким образом сотрудники могут использовать эту новую информацию для улучшения обслуживания пациентов и снижения времени ожидания?
Первое, что нужно сделать, – стабилизировать систему. Инструментом для этого послужит WIP-лимит. Сотрудники будут использовать канбан-практику эволюционного развития и экспериментальное улучшение путем определения WIP-лимита в качестве отправной точки. Посмотрев на данные, каждый решает установить для приемного покоя WIP-лимит, равный 6. Но это возможно при одном условии: врачи должны согласиться, что если там собирается шесть пациентов, то администраторы должны позвонить тем, кому назначено позднее, и попросить их перенести встречу (стараясь найти такое время, чтобы не нанести ущерба здоровью пациента). Кроме того, администраторы предложат ожидающим добровольно перенести визит, обещая при этом выбрать приоритетное для них время. Этой
Потребуется приложить немного усилий, но через несколько дней сотрудники клиники привыкают к новой политике. Они обнаруживают, что должны записывать пациентов с учетом их жалоб. Делается это посредством определения класса обслуживания: розовые стикеры будут использоваться для обозначения пациентов в более тяжелом состоянии, поэтому становится понятно, что перенести их визит невозможно. Желтые стикеры обозначают пациентов с незначительными проблемами, чей визит можно перенести. Это позволит обеспечить максимально быстрое обслуживание пациентов, которые нуждаются в этом больше всего.
И это работает! Персонал обнаружил, что, как только был введен WIP-лимит, появилась возможность записывать пациентов и после 16:00. Теперь их успеют обслужить до 18:00. Они могут планировать запись на 17:40, а пациентов с более серьезными проблемами – после 16:40 (и они придерживаются этой политики). Безусловно, если кто-то обратится в клинику с серьезной проблемой, то врач осмотрит этого пациента (или отправит в отделение неотложной помощи). Но это редкое исключение, потому что персонал клиники – умные и ответственные люди, способные принимать решения в каждом конкретном случае. Пациенты теперь выглядят намного счастливее, потому что им не приходится долго ждать.
Сотрудники офиса отнеслись к канбан-практике улучшения очень серьезно. И экспериментальным путем пришли к интересному выводу: они обнаружили, что после введения WIP-лимитов
Так что же происходит?
Сотрудники клиники обнаружили существование в стабильной системе связи между списком приема (количеством), временем обслуживания и скоростью поступления. Например, если персонал каждый час записывает 11 пациентов (так как скорость поступления λ равна 1 часу) и среднее количество в течение дня превышает семь пациентов (так как
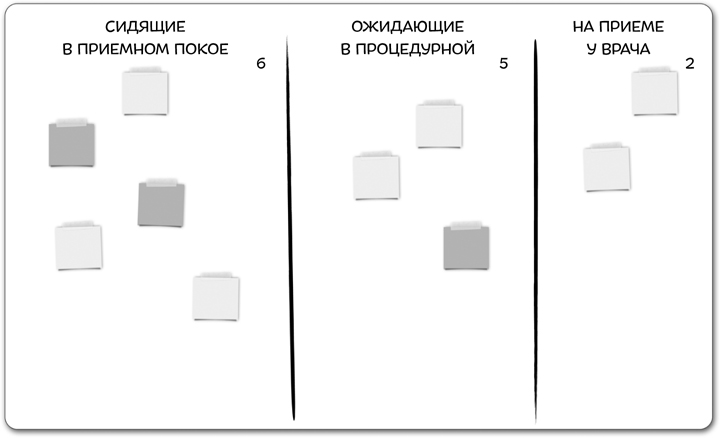
Но вдруг после ряда экспериментов они обнаружат, что планирование 10 пациентов, прибывающих каждый час, снижает список до четырех пациентов? В час пик все процедурные переполнены, но большую часть времени один пациент находится в приемном покое, один ожидает приема врача в процедурной комнате и двое – на приеме у врача:
При помощи канбан-доски, CFD и экспериментирования с WIP-лимитом сотрудники клиники обнаружили, что могли бы уменьшить время ожидания пациента почти на 15 минут только за счет сокращения записи на одного человека в час.
Это работает, потому что закон Литтла говорит нам, что в стабильной системе на время обслуживания пациента влияет две вещи: очередь и скорость прибытия. А WIP-лимиты позволяют контролировать одну из них. При добавлении WIP-лимита на канбан-доску вы можете уменьшить неравномерность, которая приводит к нагромождению в очереди. Это дает возможность сократить время обслуживания за счет снижения скорости поступления (например, удерживая работы в бэклоге до тех пор, пока команда занята выполнением текущего задания, как делают scrum-команды, или уменьшая число пациентов, записанных в течение каждого часа.
Именно так сотрудники клиники могут использовать закон Литтла для расчета среднего времени, затраченного на прием одного пациента. Но даже если они не рассчитают это время,
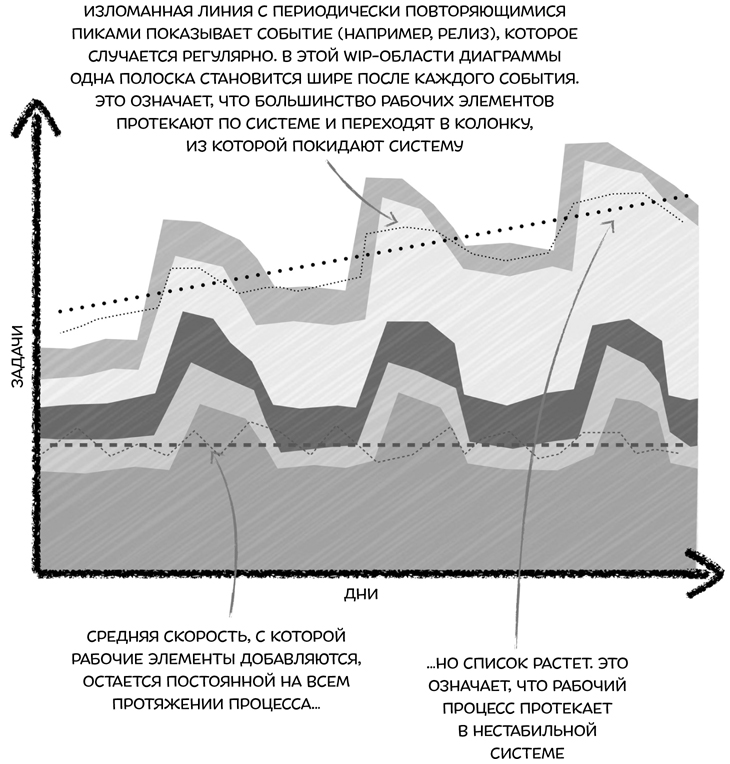
Теперь рассмотрим пример, приближенный к реальной жизни. Допустим, каждые три недели ваша команда вязнет в работе по выпуску релиза.
К сожалению, дела идут не очень хорошо. Сначала все было отлично, но со временем возникли проблемы. Несмотря на все усилия, потраченные на выполнение работы, команда чувствует, что не имеет достаточно времени на ее завершение. И каждый испытывает более сильный стресс, чем в предыдущем месяце. К тому же все знают: если они не выполнят работу максимально быстро, то в следующем месяце будет еще хуже.