2.6.3. Запоминание числовой информации

У некоторых людей возникают определенные трудности с запоминанием числовой информации, например, бывает сложно зафиксировать в памяти даже десятизначное число. Но, ознакомившись с простым и в то же время очень эффективным способом запоминания числовой информации, эту проблему можно оставить в прошлом. Более того, выполнив задание, которое мы рассмотрим в этом параграфе, запомнить, скажем, стозначное число с одного прочтения вообще не составит вам труда.

Небольшая историческая справка. Немецкий лингвист Станислав Минк фон Весншайн в 1648 г. предложил оригинальный способ запоминания числовой информации путем перевода цифр в буквы. Затем из букв создаются определенные слова, которые легко переводятся в хорошо понятные мозгу образы.

Со временем эта методика совершенствовалась, и в настоящее время существуют различные системы перевода числовой информации в образы. Этих систем не так много, и они носят следующие названия: «цифровой код», «числовой код», «букво-цифровой код», «число-буквенный код» и т. п.

Мы предлагаем свое видение данной системы, которое основывается на «Главной системе» Тони Бьюзена [3, с. 103–151]. Для простоты будем называть ее так – Система числового кодирования (числовое кодирование). На наш взгляд, система числового кодирования является максимально простой и понятной даже для школьников начальных классов.

Наши юные ученики, возраст которых достигал 8 лет, без труда осваивали эту систему ввиду ее простоты, удобства применения и, самое главное, – правильного подхода и объяснения всех особенностей и нюансов числового кодирования с нашей стороны.

После этого они с легкостью запоминали, например, 150–200 знаков числа Пи, тратя на это не более 45–60 минут.

Одна наша ученица (9 лет) принимала участие в региональных соревнованиях по мнемотехнике (январь 2020 года) и заняла там второе место среди 28 участников в своей возрастной категории (до 12 лет).

Причем никаких особых тренировок перед соревнованиями она не проводила, более того, она участвовала в таком мероприятии впервые.

Справедливости ради отметим, что нужную психологическую подготовку, а точнее, правильный настрой наша ученица получила.

А сейчас непосредственно переходим к изучению системы числового кодирования. Каждой цифре присваивается соответствующая неизменная согласная буква.

Базовая формула для перевода цифр в буквы выглядит так:

Цифра = Неизменная согласная буква.

Буквенная кодировка цифр выглядит следующим образом:

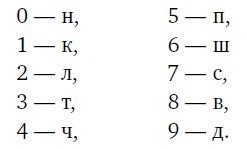
Несложно заметить, что почти все буквы, которые кодируют цифры (кроме 1 и 2) – это согласные, и они совпадают с начальным звучанием соответствующей цифры. Ноль (0) – начинается на «н», три (3) – начинается на «т», четыре – «ч», пять (5) – «п» и т. д. Но вернемся к цифрам 1 и 2. Единица начинается на гласную, второй буквой идет «д», но эта буква уже занята цифрой 9 (д), кстати, и цифра 2 также начинается на «д», поэтому поступаем следующим образом. «1» чаще всего похожа на кол, а «2» – на лебедя, следовательно, присваиваем букву «к» цифре 1 и «л» – цифре 2.

Как видите, запомнить предложенную кодировку элементарно, однако немного внимания стоит уделить цифрам 1 и 2.

Только после этого переходим к заданию, проработка которого навсегда решит все проблемы с запоминанием числовой информации.

Теперь вам предстоит создать и запомнить 100 слов (образов) по системе числового кодирования. Словосочетание «числовое кодирование» мы применяем не случайно, поскольку придумывать образы нужно именно на двузначные числа от 00 до 99.

Рассмотрим несколько характерных примеров и правила (алгоритм) подбора наиболее удачных слов.