— Так что уже пять, — сказал Барб, — только для бутылки.

— Да. Чтобы взять самый общий случай, надо добавить шестую ось, чтобы отмечать вертикальные перемещения. — Я приподнял бутылку над полом. — Так что нам нужны шесть измерений нашего конфигурационного пространства только для положения и ориентации бутылки. — Я поставил её обратно. — Но если мы ограничимся полом, то хватит и пяти.

— Ладно, — сказал Барб. Он так говорил, только когда что-нибудь окончательно понимал.

— Я рад, что ты согласен. Думать в шести измерениях трудно.

— Я думаю просто о шести колонках на моей доске вместо трёх, — сказал он. — Но я не понимаю, зачем нужно ещё шесть измерений для картофелины. Почему не воспользоваться теми шестью, которые у нас уже есть для бутылки.

— Мы ими и пользуемся, — объяснил я, — но записываем числа в отдельные колонки. Тогда каждая строка таблицы содержит в себе всё, что нам нужно знать о системе бутылка-картофелина в данный момент времени. Каждая строка — двенадцать чисел, дающих нам x, y и z бутылки, её угол отлетания от пинка, угол чтения этикетки, угол наклона и всё то же самое для картофелины, — точка в двенадцатимерном конфигурационном пространстве. И теорам это становится полезным, например, когда мы соединяем точки и получаем траектории в конфигурационном пространстве.

— Когда ты говоришь «траектория», мне представляется что-то, летящее по воздуху, — ответил Барб. — Я не понимаю, что ты имеешь в виду, когда речь о двенадцатимерном пространстве, которое вовсе и не пространство.

— Давай упростим до предела. Будем двигать бутылку с картофелиной только по оси x и забудем про вращение.

Я положил их так:

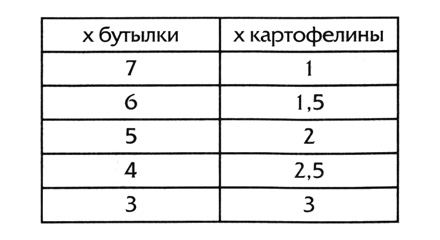
— Можешь отметить у себя на доске их координаты по оси x?

— Конечно. — И через несколько секунд Барб показал мне такую табличку:

— Сейчас я их столкну. Медленно, конечно. Постарайся записывать координаты, если успеешь.

Я начал двигать картофелину и бутылку, останавливаясь и говоря: «Отмечай» всякий раз, как хотел, чтобы он добавил новую строчку к таблице.

— Бутылка движется быстрее, — заметил Барб.

— В два раза быстрее. — Я закончил тем, что в точке с координатой 3 положил картофелину на бутылку.

— Они столкнулись, — сказал я, — и теперь начнутся разлетаться, но медленно, потому что картошка при ударе смялась и часть энергии потеряна.

С небольшими моими подсказками Барб добавил к табличке ещё несколько строк.

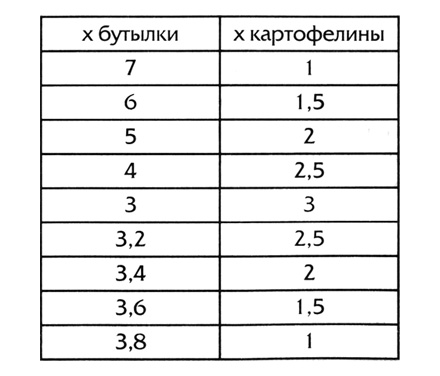
— Вот, — сказал я, отпуская соударившиеся тела и вставая с корточек. — Всё происходило на прямой, то есть ситуация одномерная, если по-прежнему думать в координатах светителя Леспера. Однако светитель Гемн сделал бы сейчас вещь, которая покажется тебе странной. Гемн считал бы, что каждая строка таблицы задаёт точку в двумерном конфигурационном пространстве.

— То есть каждая пара чисел — точка, — перевёл Барб. — Начиная с (7,1) и так далее.

— Верно. Можешь построить мне график?